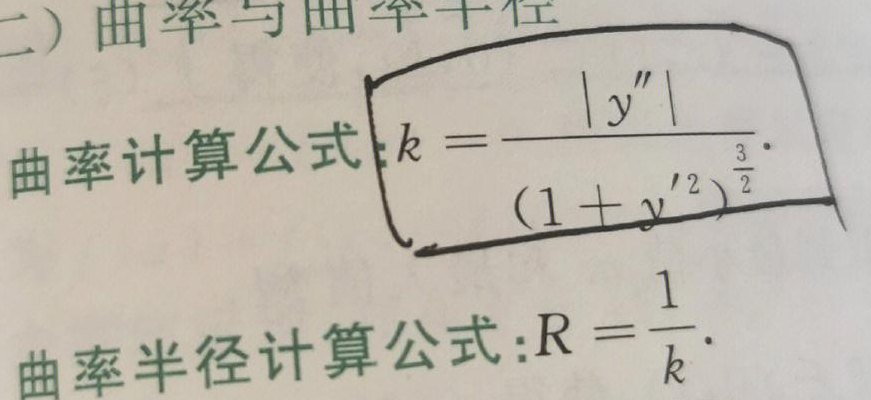曲率圆的圆心坐标公式（曲率圆心坐标怎么求）

曲率中心坐标是什么?

曲率中心坐标，在几何学中，特指曲线上某点处曲率圆的圆心坐标。这一概念对于理解曲线的局部形状特征至关重要。对于给定的曲线，其上任一点的曲率中心坐标并非固定不变，而是随着所取点的不同而变化。计算曲率中心坐标通常涉及曲线的导数（尤其是二阶导数），这些导数反映了曲线在该点处的弯曲程度和方向。

曲率中心坐标是描述曲线在某一点弯曲程度和方向的几何量，它通常用于圆或圆弧的近似描述，在微分几何、工程学、物理学和计算机图形学等领域有广泛应用。不过，曲率中心坐标并非一个固定值，而是随着曲线上点的位置变化而变化。在详细解释之前，需要了解曲率中心的基本概念。

曲率中心坐标是k=y/[(1+(y)^2)^(3/2)]。曲线的曲率就是针对曲线上某个点的切线方向角对弧长的转动率，通过微分来定义，表明曲线偏离直线的程度。数学上表明曲线在某一点的弯曲程度的数值。曲率是几何体不平坦程度的一种衡量。平坦对不同的几何体有不同的意义。

曲率中心坐标是描述曲线上某点处曲率特性的重要几何量。在微分几何中，对于一条平滑曲线，其上任一点的曲率中心定义为：通过该点并与曲线在该点具有相同切线方向和曲率圆的圆心。曲率中心坐标的计算依赖于曲线的参数方程或显式方程，以及该点的具体位置。

曲率中心坐标，曲线上任一点对应的曲率中心坐标公式的推导过程如下：曲线上点M处的曲率的倒数，称作曲线在这点处的曲率半径，记作p ，则 在点M处曲线的法线的某一侧上取一点D，使|DM|=p，并以D为圆心，以p为半径作圆。把这个圆称作曲线在点M处的曲率圆，把圆心D称做曲线在M处的曲率中心。

曲率中心坐标公式考研考吗

1、曲率中心坐标公式考研可能会考，近十年没有考过，但在1995考研数学二考过一个8分的大题，低推导曲率中心坐标的。只要大纲上有就有可能考，那么简单的一个公式记一下也不费时间，万一考了，自己做过准备也不用担心。

2、之前有考过，1995考研数学二考过一个8分的大题，低推导曲率中心坐标的，只要大纲上有就有可能考，那么简单的一个公式记一下也不费时间，万一考了，自己做过准备也不用担心。

3、曲率中心坐标公式推导如下：首先需要假设曲率k=y/[(1+(y)^2)^(3/2)]，在前面的式子中，可以假设其中y，y分别为函数y对x的一阶和二阶导数。需要进行假设曲线r(t) =(x(t)，y(t))，曲率k=(xy - xy)/((x)^2 + (y)^2)^(3/2)，然后进行求导得到第二步。

4、考研数学三曲率和方程近似解不考。因为考研数学三大纲中未做出要求。考研数学三的复习需要针对大纲有的放矢，才能事半功倍。

5、曲率中心坐标，曲线上任一点对应的曲率中心坐标公式的推导过程如下：曲线上点M处的曲率的倒数，称作曲线在这点处的曲率半径，记作p ，则 在点M处曲线的法线的某一侧上取一点D，使|DM|=p，并以D为圆心，以p为半径作圆。把这个圆称作曲线在点M处的曲率圆，把圆心D称做曲线在M处的曲率中心。

6、举个例子，假设有一个平面曲线y=f，在点处，我们想要找到其曲率中心的坐标。首先，计算函数在该点的一阶导数y和二阶导数y。然后，利用这些导数值以及点的坐标，根据曲率中心的计算公式，可以求出曲率中心的坐标。这个公式通常涉及到一些复杂的数学运算，包括除法、平方和开方等。

曲率圆方程怎么求

1、曲率圆方程的表达式：(x-α)^2+(x-β)^2=R^2。其中R是曲线y=f(x)在P(x0，y0)点处的曲率半径，圆心(α，β)称为曲线y=f(x)在P(x0，y0)点处的曲率中心，且α=x0-f(x0){1+[f(x0)]^2}/f(x0)，β=y0+{1+[f(x0)]^2}/f(x0)。

2、曲率圆方程的表达式：（x-α）^2+(x-β）^2=R^2。曲率圆，又称密切圆。在曲线上一点M的法线上，在凹的一侧取一点D，使DM等于该点处的曲率半径，以D为圆心，DM为半径作圆，这个圆叫做曲线在点M处的曲率圆。在点M附近，曲率圆弧与曲线弧密切程度非常好，所以曲率圆又叫密切圆。

3、曲率圆方程是描述曲线在某一点处的曲率的数学公式。求解曲率圆方程的方法主要有以下几步：确定曲率半径：首先，我们需要找到曲线在给定点处的曲率半径。曲率半径是曲率圆的半径，它反映了曲线在该点处的弯曲程度。曲率半径的计算公式为R=|dθ/ds|，其中θ是曲线在该点处的角度，s是弧长。

4、圆方程曲率a=根号2/2，那曲率半径R=根号2，此点的切线斜率为k=-1，则此点法线的斜率为k=1，且曲率圆圆心在法线上，且距(1，1)的距离为曲率半径R=根号2，故易知圆心坐标为(2，2)，故可知此圆方程。曲率圆又称密切圆。

5、曲率圆方程求解步骤如下：确定曲线的参数方程 曲率圆的求解需要知道曲线在某一点的参数方程，包括x、y和z的表达式。这些参数通常表示曲线在该点的切线和法线方向。计算曲线在该点的导数 导数可以描述曲线在该点的弯曲程度和方向，对于三维空间中的曲线，需要计算x、y、z三个方向的导数。

6、曲率圆方程的表达式：（x-α）^2+(x-β）^2=R^2。曲线上点M处的曲率的倒数，称作曲线在这点处的曲率半径，记作p ，则在点M处曲线的法线的某一侧上取一点D，使|DM|=p，并以D为圆心，以p为半径作圆。把这个圆称作曲线在点M处的曲率圆，把圆心D称做曲线在M处的曲率中心。