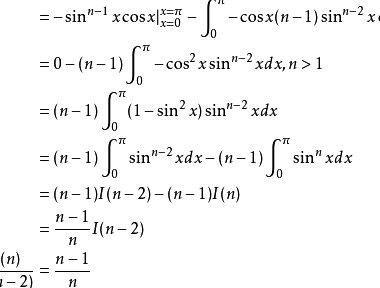华里士公式使用条件（华里士公式可以直接用吗）

CISP通过率多少？

1、cisp考试的通过率怎么样？整体的通过率很低在20~30%之间，单科考试的通过率在40%左右。这个是全国的平均水平，其实主要还是看个人了，很多人报名后就没有时间去看书听课的，而且还有不少人都缺考。导致了通过率很低下。

2、CISP（国家注册信息安全专业人员）是国内最具影响力的认证之一，拥有92%的高通过率，适用于多个行业。CISSP（国际注册信息系统安全专家）是国际上最具认可度的认证，适合企业信息安全负责人员及技术人员。

3、整体通过率在20%到30%之间，单科考试的通过率大约为40%。这反映了全国平均水平，但实际情况还取决于个人努力。许多人报名后由于时间紧张，未能投入足够的时间去学习和准备，还有部分考生因故未能参加考试，这些因素都导致了较低的通过率。

4、CISP的通过率通常在80%到95%之间，这取决于考生的准备情况和实践经验。CISP考试侧重于基础知识和技能的应用，对于那些长期从事信息安全工作的专业人士来说，通过考试通常是轻而易举的。

5、CISP包含培训、考试与题库支持。当前有优惠活动，可加入指定群组获取。通过率高达99%，确保实力获得认证。此大纲针对我国国情与实际需求，确保覆盖CISE、CISO和CISM的全部知识要点，是教材编制、讲师教学与学员学习的重要参考依据。知识体系采用组件模块化结构，包含知识域、知识子域与知识点三个层次。

6、纸质证书在成绩公布后3个月发放。CISP证书有效期为3年，每3年需进行一次维护，年金为500元，三年一交。目前，CISP官方报名费用为12800元，享有75折优惠，包括培训、考试、年金、教材和证书费用。赛虎学院教学质量有保证，学员通过率高达99%，如有疑问，欢迎通过电话咨询，知乎平台的回复可能会有所延迟。

华里士公式(点火公式)与区间再现公式

1、华里士公式，表达式为n为正偶数时为（2*n）/(2*n-1)*(2*n+1)*...*3*1，n为正奇数时为（2*n-1）*（2*n-3）*...*1。双阶乘n！表示从n下降到1的每个偶数或奇数的乘积，取决于n的奇偶性。区间再现公式指出，对于连续函数f(x)，将其积分可表示为（f(a)+f(b)）/2*(b-a)。

2、∫（0，π）xf（sinx）=π/2∫(0，π）f（sinx）类似于华里士公式（俗称的点火公式），用区间再现的方法令x=π-t即可证出，这里就是用了这个公式，将x变成了外面的π/2，其中cos^2也可以看做sinx的函数。

算一个定积分,用华里士公式?

不能用华里士公式（这公式是0到π/2区间的积分），只能由(sinx)^4=[(1/2)(1-cos2x)]^2=(1/4)(1-2cos2x+(cos2x)^2)=(1/4)(1-2cos2x+(1/2)(1-cos4x))，再求出原函数计算定积分。

华里士公式：所以 ∫(0→π/2) (sinx)^4 = 3/4 * 1/2 * π/2 = 3π / 16 (sinx)^4周期是sinx的周期的一半，即T = π，并且函数值始终为正值。（这个可以直观感受，也可以降幂求周期(sinx)^4 = [3 - 4 cos(2x)+ cos(4x)]/8）所以所求积分是n=4的华里士积分的4倍。

解：华里士公式（Wallis公式）是对(sinx)^n在区间[0，π]的积分不等式，有递推式I(n)=∫[0，π](sinx)^ndx=[(n-1)/n]I(n-2)。(1)题，将积分区间拆成[0，π]∪[π，2π]，易得，原式=2I(4)=2*3/4I(2)=3/4I(0)，而I(0)=π，∴原式=3π/4。(3)题。

定积分的计算中，掌握一些巧妙的方法能够简化计算过程。

重要公式/ 区间再现公式/： 这个公式揭示了积分与区间的关系，是理解积分基本性质的基础。具体的证明过程在文章的最后部分详述，帮助我们深入理解。 华里士公式（Wallis公式）/： 这个经典公式在特定条件下能简化复杂的积分，它的威力不容小觑。让我们一起揭开它的神秘面纱。