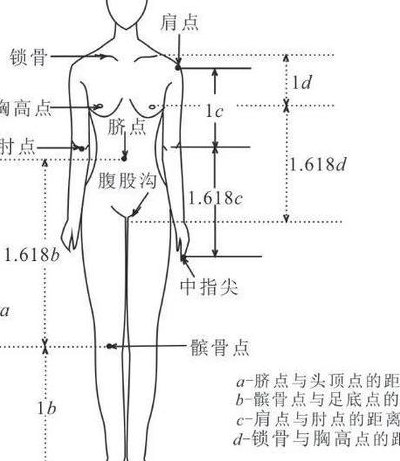
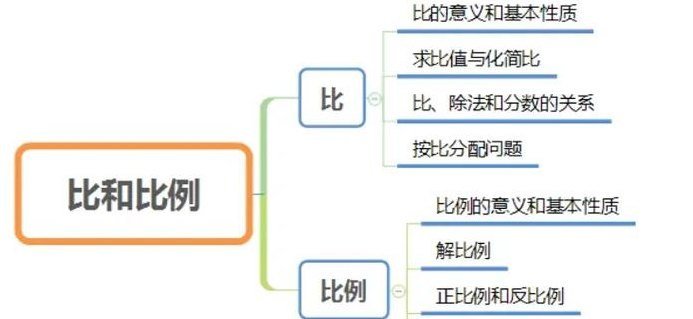
比例的各部分名称（比例的各部分名称示意图）

比和比例的意义是什么?各部分名称是什么?基本性质及作用是什么?_百度...

1、比的意义：两个数相除，称为这两个数的比，用以表示它们之间的关系。比号前面的数称为比的前项，比号后面的数称为后项，相除的结果称为比值。 比的性质：比的前项和后项同时乘或除以相同的数（0除外），比值保持不变。这一性质在化简比和求比值时尤为重要。

2、比的意义：将两个数相除的行为称为它们的比，这是表示两个数相除的一种方式。在这个行为中，位于比号前面的数称为比的前项，位于比号后面的数称为比的后项，相除的结果被称为比值。 比例的意义：当两个比的比值相等时，这两个比组成的式子称为比例。比例是一个等式，其中包括至少两个比。

3、比的意义：两个数相除，叫做这两个数的比。表示两个数相除。比号前面的数叫比的前项，后面的数叫做后项，相除的结果叫做比值。比例的意义： 表示两个比相等的式子叫做比例。 是一个等式。比例两端的两项叫做比例的外项，中间的两项叫做内项。

4、意义、项数、各部分名称不同：- 比表示两个数相除，只有两个项，称为比的前项和后项。- 比例是一个等式，表示两个比相等，有四个项：两个外项和两个内项。 基本性质和应用不同：- 比的基本性质是：比的前项和后项都乘以或除以一个不为零的数，比值不变。这一性质用于化简比。

5、比的意义：两数相除就叫做这两数的比。比的基本性质：比的前项和后项同时乘或者除以相同的数（0除外），比值不变。以“3：5=0.5为例“3”叫做比的前项，“5”叫做比的后项，“0.5”叫比值。比例的意义：表示两个比相等的式子叫比例。

分数形式的比例怎么确定他们的名称

分数形式的比例的各部分名称：组成比例的四个数，叫做比例的项。两端的两项叫做比例的外项，中间的两项叫做比例的内项。

解比例的方法：依据比例的基本性质，将比例转化为外项之积等于内项之积的形式，然后通过解方程来确定未知项的值。 解分数形式比例的方法：先进行交叉相乘，将比例式转换为等积式，接着通过解方程来找出未知项的值。

这里需要结合具体的例子进行说明，比如含有未知数的比例，2：5=6：x。在比例2：5=6：x中，2与x成为比例的外项，5与6成为比例的内项。比例的根本性质是两个外项的积等于两个内项的积，因此对于含有未知数的比例2：5=6：x转化为方程式为2x=5×6，解得x=15。

把比例写成分数形式时，第一个分数的分子和第二个分数的分母是外项，第一个分数的分母和第二个分数的分子是内项。例如：4：5=16：20 写成分数的形式是：4/5=16/20 其中4和20是外项，5和16是内项。

分数表示一个数是另一个数的几分之几，或一个事件与所有事件的比例。把单位“1”平均分成若干份，表示这样的一份或几份的数叫分数。分子在上，分母在下。历史：最早的分数是整数倒数：代表二分之一的古代符号，三分之一，四分之一，等等。埃及人使用埃及分数c。 1000 bc。

小学六年级比例知识点

1、六年级比例的知识点归纳如下：比例的意义：表示两个比相等的式子叫做比例。

2、百米赛跑，路程100米不变，速度和时间是反比例。排队做操，总人数不变，排队的行数和每行的人数是反比例。做纸盒子，总个数一定，每人做的个数和人数。总价一定，它的单价和数量是反比例。长方形的面积一定，长和宽是反比例。总价一定，单价与数量成反比例。

3、比例尺：一幅图的图上距离和实际距离的比，叫做这幅图的比例尺。图上距离：实际距离=比例尺 图上距离与实际距离的单位要统一。解比例的意义：求比例中的未知项，叫做解比例。

4、六年级比例知识点归纳如下：比例的意义 比例反映的是两个比相等的数学关系，通常表示为a：b = c：d。 比例中的两个比的比值必须相等，这被称为比例的相等性原则。 比例与比的区别在于，比是由两个数直接相除得到的，而比例是比较两个比的比值。