什么是实数和虚数（什么是实数和虚数?）

昨天 6阅读

什么是实数和虚数

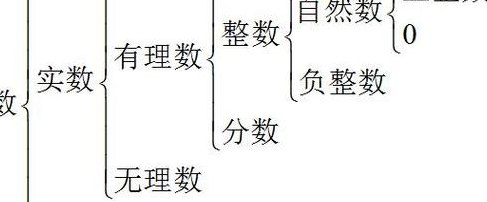
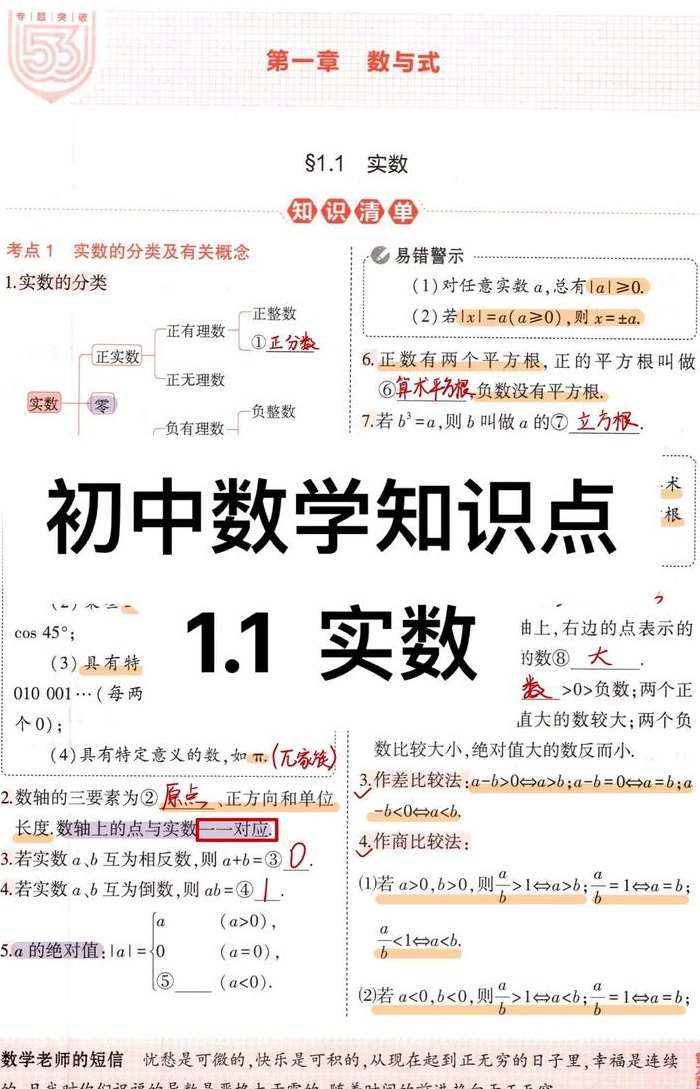
1、实数（realnumber）是有理数和无理数的总称。实数定义为与数轴上的实数，点相对应的数。实数可以直观地看作有限小数与无限小数，实数和数轴上的点一一对应。但仅仅以列举的方式不能描述实数的整体。实数和虚数共同构成复数。实数可以分为有理数和无理数两类，或代数数和超越数两类。

2、实数是指那些在数轴上可以找到，从负无穷大到正无穷大的数。虚数则是带有虚数单位i的数，即\( i = \sqrt{-1} \)。通过虚数单位i，我们可以表示数轴上不存在的点，例如\( -10 \)和\( 3+5i \)都是虚数。

（图片来源网络，侵删）

3、实数和虚数是数学中的基本概念。实数，即有理数和无理数的总称，它们与数轴上的点一一对应，可以理解为有限小数、无限小数或代数数和超越数。实数集用R表示，是不可数的，是实数理论研究的核心内容。实数系是指所有实数的集合，是完备的阿基米德有序域，具有唯一性。

1、答案：实数是可以与数轴上的点一一对应的数，包括有理数和无理数。虚数是一种数学上的概念，定义为实部为实数，虚部为数学符号的平方根的复数。纯虚数则是虚部不为零，而实部为零的虚数。详细解释：实数是最常见的数值类型之一，它们包括有理数和无理数。

2、纯虚数是虚数的一种特殊形式。一个纯虚数的定义是，它的实数部分为0，只有虚数部分非零。也就是说，纯虚数的形式可以表示为纯粹的bi。它们在复数理论中具有重要的地位，尤其是在数学分析和物理学的某些领域中有着特定的应用。纯虚数的存在丰富和扩展了数学和科学的理论体系。

3、复数就是实数和虚数的总称。所有的数都是复数。实数是有理数和无理数的总称表示为 a。虚数是复数中除了实数的数。在复数域中，负数-1的平方根记为i(即i2=-1)，称为虚数或虚数单位。一个实数乘以i称为纯虚数，例如5i 就是一个纯虚数。

（图片来源网络，侵删）

实数与虚数的概念：实数是指可以在数轴上表示的数，包括有理数和无理数。有理数包括整数、正数、负数和分数。无理数则是不能表示为分数形式的数，如和根号下的非完全平方数等。实数最大的特性是可以进行算数运算，如加法、减法、乘法和除法等，并且运算结果仍然是一个实数。

实数虚数的概念具体如下：实数：实数是有理数和无理数的总称。有理数包括整数和分数，无理数则是无限不循环小数。实数与数轴上的点一一对应，因此也被称为“实在的数”。实数集合通常用字母R或Rn表示，其中Rn表示n维实数空间。

实数：有理数和无理数的总称。其中无理数就是无限不循环小数，有理数就包括整数和分数。虚数：在数学里，将平方是负数的数定义为纯虚数。所有的虚数都是复数。这种数有一个专门的符号“i”(imaginary)，它称为虚数单位。定义为i^2=-1。

实数和虚数是数学中的基本概念。实数，即有理数和无理数的总称，它们与数轴上的点一一对应，可以理解为有限小数、无限小数或代数数和超越数。实数集用R表示，是不可数的，是实数理论研究的核心内容。实数系是指所有实数的集合，是完备的阿基米德有序域，具有唯一性。

实数是实数理论的核心研究对象。所有实数的集合则可称为实数系（realnumbersystem）或实数连续统。任何一个完备的阿基米德有序域均可称为实数系。在保序同构意义下它是惟一的，常用R表示。由于R是定义了算数运算的运算系统，故有实数系这个名称。虚数。

在数学里，如果有某个数的平方是负数的话，那个数就是虚数了。所有的虚数都是复数。

2、实数是指可以在数轴上表示的数，包括有理数和无理数。有理数包括整数、正数、负数和分数。无理数则是无法表示为分数形式的数，如和根号下的非完全平方数等。虚数是数学中的概念，以字母i来表示。虚数的形式是实数之外不能与实数相等或相减的数，即平方根下包含负数的数值解表达形式。

4、实数：有理数和无理数的总称。其中无理数就是无限不循环小数，有理数就包括整数和分数。虚数：在数学里，将平方是负数的数定义为纯虚数。所有的虚数都是复数。这种数有一个专门的符号“i”(imaginary)，它称为虚数单位。定义为i^2=-1。

免责声明：本文来自网友投稿，不代表苦迪号的观点和立场，如有侵权请联系本平台处理。