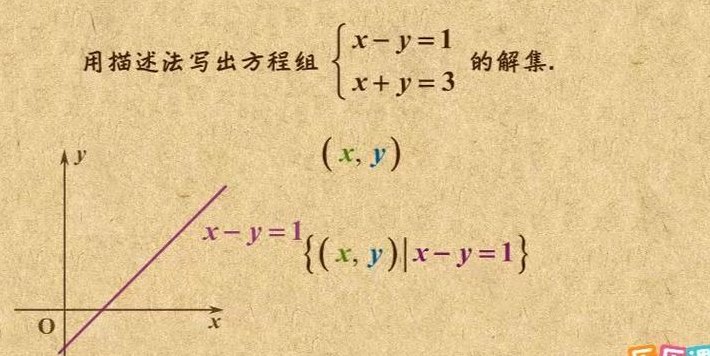所有正奇数组成的集合（所有正奇数组成的集合用描述法表示）

所有正奇数组成的集合用描述法表示

1、所有正奇数组成的集合用描述法表示：{X│X=2N+1，N表示自然数}。奇数就是被2除余1的数，2N+1（N为整数）就表示了奇数，考虑到正奇数，要求N=0，所以又有N为自然数。

2、所有正奇数组成的集合：{x∣x=2n+1，n∈N}或者{正奇数} 集合的表示方法有：枚举法，描述法，文氏图法，区间法。

3、（1）用描述法表示为｛x|x=n^2，n∈N，0n6｝ (2){n|n=2k+1，k∈N} 打字不易，如满意，望采纳。

4、用描述法表示奇数的集合，先要知道什么是集合，什么是奇数。集合是指具有某种特定性质的具体的或抽象的对象汇总成的集体，这些对象称为该集合的元素。奇数：在整数中，不能被2整除的数叫做奇数。奇数可以分为正奇数和负奇数。

集合的表示法怎么理解?

1、集合三种表示方法是：列举法、描述法、图示法。集合的含义是：集合是一定范围的，确定的，可以区别的事物，当作一个整体来看待，就叫做集合，简称集，其中各事物叫做集合的元素或简称元，是具有某种特定性质的事物的总体。列举法：把集合中的元素一一列举出来，并用花括号“{}”括起来表示集合的方法。

2、集合表示法有：穷举法，就是把集合中的元素全部表示出来，如{1，2}。表达式法，如{x|x1}。图示法。常用于表示无限集合，把集合中元素的公共属性用文字，符号或式子等描述出来，写在大括号内，这种表示集合的方法叫做描述法。

3、描述法是集合的常用表示方法。描述法的定义﹕常用于表示无限集合，把集合中元素的公共属性用文字﹐符号或式子等描述出来﹐写在大括号内﹐这种表示集合的方法叫做描述法。

4、集合的表达方法通常有以下四种：列举法：按照任意一种次序，不重复的列举出集合的全部元素，并且用花括号括起来。部分列举法：列出一部分元素，但是这部分元素可以表示一定客观规律的元素未列举出来的元素用……表示。命题法：用一个和x有关的命题来定义集合。

三、用适当的方法表示下列集合。

所有正奇数组成的集合。{x|x=2n+1；n∈N} 方程x+3x-4=0的解集。(x+4)(x-1)=0； x=-4或x=1； {x|x=-4或x=1} 大于5的所有偶数组成的集合。{x|x5且x=2n；n∈N} 绝对值小于4的所有实数组成的集合。{x||x|4} 不等式2x-53的整数解集。

这两个一次函数的图像分别是根直线，并且一个斜率是1一个斜率是-2，不平行，那么图像交点就是个点。

y=x^2-2x+3=(x-1)^2+2=2，所以二次函数y=x^2-2x+3的函数值组成的集合可以表示为：{y|y=2}；要使y=3/(x^2-2)有意义，x^2-2不等于0，所以函数y=3/(x^2-2)的自变量的值组成的集合为：{x|x不等于-根号2且x不等于根号2}。

使学生弄清楚三种表示方式的优缺点和体会它们存在的必要性和适用对象。设计意图：明确集合元素的三大特性，使学生弄清楚三种表示方式的优缺点，从而突破难点。

全部的奇数有哪些?偶数有哪些?质数有哪些?合数有哪些?

全部奇数：奇数是指不能被2整除的整数，例如：9等。任意两个连续的整数中，其中一个必定是奇数。在整数中，所有正奇数可以表示为形如 2n + 1 的形式，其中 n 是整数。类似地，负奇数可以表示为形如 2n - 1 的形式。简单地说，奇数就是形如 2n 1 的整数集合。

-100的奇数：1111122222333334444455555666667777788888999999。

偶数（也叫双数）：能被2整除的数。如：0 、2 、 4 、 6 、 8 、 10 ………奇数（也叫单数）：不能被2整除的数。如：1 、3 、 5 、 7 、 9………质数（也叫素数）：只有1和本身两个因数的数。如：2 、1117………合数：除了1和本身，还有其他因数的数。

奇数和偶数，这个不用一一列举了吧。奇数，1，3，5，7，9，...，99 偶数，2，4，6，8，10，...，100 质数：1111223344455667778897 合数，100以内所有的自然数，除去1和上面的质数。

有哪些所有奇数组成的集合的例子?

1、所有奇数组成的集合：奇数可以用2n+1或2n-1来表示（n是整数）。所以所有奇数组成的集合就是{x|x=2n+1，n∈Z}。奇数（odd）指不能被2整除的整数 ，数学表达形式为：2k+1， 奇数可以分为正奇数和负奇数。

2、综上所述，所有的奇数集合包括了所有的正奇数和负奇数。他们的特性就是无法被2整除。举例说明有：奇数包括所有形如 2n 1 的整数集合。例如：正奇数有 7 等。负奇数则为它们的相反数。如：----7 等。他们的共同特性是无法被偶数整除的数。

3、用列举法写出大于-5且小于9的所有奇数组成的集合为：{-3，-1，1，3，5，7} 列举法：将集合中的元素一一列出来（在列举时不考虑元素的顺序），并且写在大括号内的 一种表示集合的方法。