平均值的标准偏差（平均值的标准偏差是相对标准偏差吗）

有比较好的边缘计算公司参考吗？

Aarna Networks，一家位于印度和加州圣何塞的边缘计算公司，专注于5G和边缘计算应用的自动化软件开发。Aarna推出的多集群协调平台（AMCOP）支持5G网络服务和边缘计算应用的协调、生命周期管理和实时政策驱动的自动化。2022年初，Aarna宣布计划扩充其在印度的工程团队，招募更多专业技术人才。

深信服科技创新智能边缘计算平台，提供高效云边协同能力，构建云边安全协同，提供端-边-云完整安全方案，打造安全可信的边缘计算平台。江行智能融合边缘计算与人工智能技术，专注研发边云协同智能物联网解决方案，拥有覆盖电力能源数智化技术团队，为14家世界500强企业服务。

国内目前在边缘计算领域比较好的公司有：阿里云 百度智能云 移动云 网心科技 天翼云 基本算是国内五虎。

平均值的标准偏差时如何计算的?

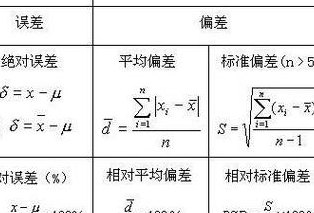
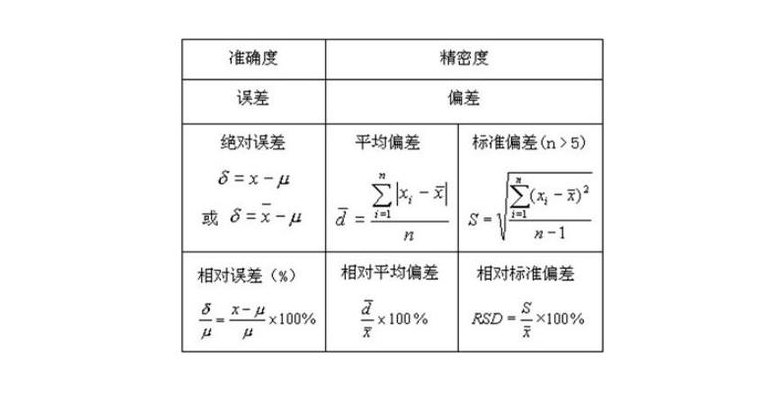
平均值的标准差的计算公式：S=Sqr（∑（xn-x拨）^2/（n-1）），公式中∑代表总和，x拨代表x的算术平均值，^2代表二次方，Sqr代表平方根。平均值的标准偏差是指一种度量数据分布的分散程度之标准，用以衡量数据值偏离算术平均值的程度。标准偏差越小，这些值偏离平均值就越少，反之亦然。

平均值的标准偏差时相对于单次测量标准偏差而言的，在随机误差正态分布曲线中作为标准来描述其分散程度：在一定测量条件下（真值未知），对同一被测几何量进行多组测量(每组皆测量N 次)，则对应每组N 次测量都有一个算术平均值，各组的算术平均值不相同。

平均标准偏差的计算公式是s=sqrt （（（x1-x）^2+ （x2-x）^2+……（xn-x）^2）/（n-1））。标准偏差是一种度量数据分布的分散程度之标准，用以衡量数据值偏离算术平均值的程度。标准偏差越小，这些值偏离平均值就越少，反之亦然。标准偏差的大小可通过标准偏差与平均值的倍率关系来衡量。

实验标准偏差的计算步骤如下：计算样本的平均值\bar{x}。计算每个数据点与平均值的差(x_i-\bar{x})。将每个差求平方(x_i-\bar{x})^2。求出所有平方差的平均数\frac{1}{N-1}\sum_{i=1}^{N}(x_i-\bar{x})^2。将步骤4的结果开方，得到实验标准偏差s。

样本标准偏差 ， 代表所采用的样本X1，X2，...，Xn的均值。总体标准偏差 ， 代表总体X的均值。例：有一组数字分别是200、50、100、200，求它们的样本标准偏差。

测得值 计算法 测量技术 【在测量技术以及统计管理中，求算术平均值X与标准偏差σ都是必需要的计算，本文就适合不同情况的几种x、σ计算方法作一介绍。

平均绝对误差,标准偏差和平均值的标准偏差有什么区别

1、简而言之，平均绝对误差侧重于预测的准确性，标准偏差关注数据的波动情况，而平均值的标准偏差则衡量均值的精确度。理解这些概念之间的区别有助于我们在数据分析中做出更合理的判断。在实际应用中，我们经常需要对这些统计指标进行比较，以便更好地理解数据的特征。

2、标准偏差是描述随机变量值围绕均值波动程度的指标。数值大小反映出数据分布的分散度，数值越大表示数据波动越大，反之则越集中。标准误差（Standard Error）衡量的是样本均值与总体均值之间的差异，用于反映样本均值的可靠性。当总体标准差未知时，常用样本标准差来估计标准误差。

3、平均绝对误差衡量的是预测值与实际值之间的平均差距，它能直观地反映出预测的准确性。标准偏差则用于衡量一组数据相对于其平均值的离散程度，数值越大说明数据波动越大，反之则越稳定。平均值的标准偏差具体是指一组独立同分布的随机变量均值的波动性，用来评估均值的精确度。

4、平均绝对误差是指你的预测值与真实值之间平均相差多大。标准偏差就是描述在均值周围的波动情况。大则表示你的分布范围广且散；小则表示你的分布范围窄且聚集。平均值的标准偏差是用来表示一组独立同分布的随机变量的均值的波动性，也就是均值的精确度。

5、在评估测量结果的精度时，平均绝对误差是一个重要的指标。它表示所有测量值与真实值之差的绝对值的平均值。平均绝对误差能够直观地反映测量结果与真实值之间的平均偏差，具有较好的可解释性。综上所述，通过平均误差、标准差、均方差以及绝对值的计算，我们可以全面评估测量结果的精度和波动情况。

平均值的标准偏差的计算公式

平均值的标准偏差的计算公式如下：公式：sqrt^2+^2+^2)/)，其中 x1， x2，， xn 是样本数据，x 是样本的平均值，n 是样本数量， 是自由度，sqrt 表示开平方。解释：这个公式是用来计算样本数据相对于其平均值的标准偏差的。

平均值的标准偏差的计算公式：sqrt(((x1-x)^2+(x2-x)^2+...(xn-x)^2)/(n-1))=STDEV.S(x1，x..xn)。由于方差是数据的平方，与检测值本身相差太大，人们难以直观的衡量，所以常用方差开根号换算回来这就是我们要说的标准差。

平均值的标准差的计算公式：S=Sqr（∑（xn-x拨）^2/（n-1）），公式中∑代表总和，x拨代表x的算术平均值，^2代表二次方，Sqr代表平方根。平均值的标准偏差是指一种度量数据分布的分散程度之标准，用以衡量数据值偏离算术平均值的程度。标准偏差越小，这些值偏离平均值就越少，反之亦然。

平均值的标准偏差是什么?

平均值的标准偏差是衡量样本数据变化范围的统计量。 平均值表示数据的中心位置或集中趋势，计算方法是总和除以数量。 标准偏差反映数据集的离散程度，小标准偏差表示数据集中，大标准偏差表示数据分散。 标准偏差用于评估数据的可靠性和稳定性，计算涉及样本数据和样本数量。

平均值的标准偏差是指一种度量数据分布的分散程度之标准，用以衡量数据值偏离算术平均值的程度。标准偏差越小，这些值偏离平均值就越少，反之亦然。标准偏差的大小可通过标准偏差与平均值的倍率关系来衡量。

平均值的标准偏差，指的是这由这一系列测量结果计算得到的平均值，与待测量的真值之间的偏差程度；所以一般来说，前者没啥卵用，你可以把它当作用以推导平均值的标准偏差过程中的副产品；“平均值的标准偏差”才是我们想要的东西，毕竟我们想知道我们这次的实验结果与真值的相近程度。

平均值的标准偏差是一种衡量数据分布离散程度的统计量，它描述了数据值偏离算术平均值的程度。通常来说，标准偏差越小，数据集中的数值越集中，反之则数据分散程度越大。标准偏差的大小可以通过它与平均值的比例来衡量。

平均绝对误差衡量的是预测值与实际值之间的平均差距，它能直观地反映出预测的准确性。标准偏差则用于衡量一组数据相对于其平均值的离散程度，数值越大说明数据波动越大，反之则越稳定。平均值的标准偏差具体是指一组独立同分布的随机变量均值的波动性，用来评估均值的精确度。