向量积的几何意义（向量积的几何意义垂直关系）

向量积的几何意义是什么呢

向量积的几何意义如下：计算两个向量之间的空间关系，包括求解两个向量的夹角、向量的投影等。向量积也称为叉积或矢积。

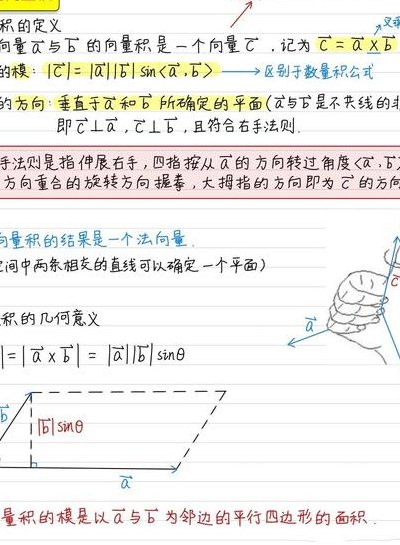
向量积的几何意义，简而言之，是衡量两个向量在三维空间中形成的平行四边形面积。具体而言，两个向量a与b的叉乘|a×b|代表了以这两个向量为边的平行四边形的面积大小。这一概念在数学中被广泛应用于几何问题的求解。进一步延伸，向量积在三维空间中的应用更为广泛。

向量内积a·b指的是两个向量对应坐标值相乘后相加的结果，它是一个数值。这个数值实际上等于两个向量长度的乘积与它们夹角余弦值的乘积。从几何学的角度来看，向量内积不仅能够帮助我们计算两个向量之间的夹角，还有一种特殊情况，那就是如果两向量的内积为零，那么这两个向量就是垂直的。

a向量与b向量的向量的积的方向与这两个向量所在平面垂直即为向量的积的几何意义。向量的积，数学中又称外积、叉积，物理中称矢积、叉乘，是一种在向量空间中向量的二元运算。与点积不同，它的运算结果是一个向量而不是一个标量，并且两个向量的叉积与这两个向量的和垂直。

换句话说，向量积表示了两个向量之间的交叉程度或者说两个向量互相垂直的程度。如果两个向量平行或者夹角为零，则它们的向量积为零；如果两个向量夹角为90度，则它们的向量积大小等于两个向量长度之积。

向量内积(点乘)和外积(叉乘)概念及几何意义

内积（点乘）几何意义：表示向量之间的角度，通过公式 ab=|a||b|cos(θ) 可判断两向量方向：ab0表示方向基本相同；ab=0表示正交，相互垂直；ab0表示方向基本相反。

向量内积代表两个向量对应坐标值相乘后相加，得到的是一个数，数值上等于两向量长度积乘以夹角的余弦。几何上的应用：两向量外积等于以两向量为邻边的平行四边形面积，方向为两向量所在平面的法线方向；外积为0，说明两向量平行。

点乘，又称内积，是两个向量的数量积。它是一个实数，表示两个向量在数量上的积合作用。例如：a·b = |a|·|b|·cos，其中表示向量a和b之间的夹角。 叉乘，又称外积，是两个向量的向量积。

向量积的几何意义

向量积的几何意义如下：计算两个向量之间的空间关系，包括求解两个向量的夹角、向量的投影等。向量积也称为叉积或矢积。

向量积的几何意义，简而言之，是衡量两个向量在三维空间中形成的平行四边形面积。具体而言，两个向量a与b的叉乘|a×b|代表了以这两个向量为边的平行四边形的面积大小。这一概念在数学中被广泛应用于几何问题的求解。进一步延伸，向量积在三维空间中的应用更为广泛。

向量积，数学中又称外积、叉积，物理中称矢积、叉乘，是一种在向量空间中向量的二元运算。与点积不同，它的运算结果是一个向量而不是一个标量。并且两个向量的叉积与这两个向量和垂直。其应用也十分广泛，通常应用于物理学光学和计算机图形学中。

向量内积a·b指的是两个向量对应坐标值相乘后相加的结果，它是一个数值。这个数值实际上等于两个向量长度的乘积与它们夹角余弦值的乘积。从几何学的角度来看，向量内积不仅能够帮助我们计算两个向量之间的夹角，还有一种特殊情况，那就是如果两向量的内积为零，那么这两个向量就是垂直的。

换句话说，向量积表示了两个向量之间的交叉程度或者说两个向量互相垂直的程度。如果两个向量平行或者夹角为零，则它们的向量积为零；如果两个向量夹角为90度，则它们的向量积大小等于两个向量长度之积。

另一种向量积分是外积，即叉积。外积在高等数学中应用广泛，不仅可以解决上述问题，还能用于计算向量在三维空间中的垂直方向，以及求解旋转和平移等问题。外积的概念和应用对于理解三维几何结构至关重要。通过掌握这两种向量积分的计算方法和应用，可以为解决复杂几何问题提供强大的工具。

向量积的几何意义是什么

1、向量积的几何意义如下：计算两个向量之间的空间关系，包括求解两个向量的夹角、向量的投影等。向量积也称为叉积或矢积。

2、向量内积a·b指的是两个向量对应坐标值相乘后相加的结果，它是一个数值。这个数值实际上等于两个向量长度的乘积与它们夹角余弦值的乘积。从几何学的角度来看，向量内积不仅能够帮助我们计算两个向量之间的夹角，还有一种特殊情况，那就是如果两向量的内积为零，那么这两个向量就是垂直的。

3、向量积的几何意义，简而言之，是衡量两个向量在三维空间中形成的平行四边形面积。具体而言，两个向量a与b的叉乘|a×b|代表了以这两个向量为边的平行四边形的面积大小。这一概念在数学中被广泛应用于几何问题的求解。进一步延伸，向量积在三维空间中的应用更为广泛。

4、a向量与b向量的向量的积的方向与这两个向量所在平面垂直即为向量的积的几何意义。向量的积，数学中又称外积、叉积，物理中称矢积、叉乘，是一种在向量空间中向量的二元运算。与点积不同，它的运算结果是一个向量而不是一个标量，并且两个向量的叉积与这两个向量的和垂直。

5、换句话说，向量积表示了两个向量之间的交叉程度或者说两个向量互相垂直的程度。如果两个向量平行或者夹角为零，则它们的向量积为零；如果两个向量夹角为90度，则它们的向量积大小等于两个向量长度之积。

6、向量数量积的几何意义是指一个向量在另一个向量上的投影。具体来说，当我们将一个向量u与另一个向量v进行点积操作时，得到的结果实际上反映了u在v方向上的投影长度与v自身长度的乘积。这种表述不仅简洁明了，而且直观地展示了两个向量之间的相互作用。