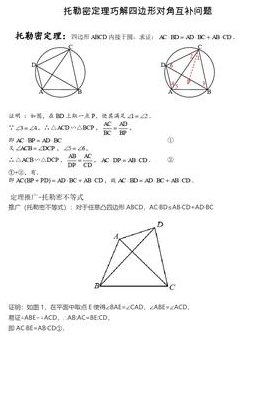
托勒密定理(托勒密定理：两对角线和为恒定值的平行四边形对角线乘积相等)

托勒密定理：证明的历史和应用

托勒密定理是数学中的一条重要定理，也是初中数学中重要的基础性定理之一。该定理是由古希腊数学家托勒密在其所写的《阿尔马吉斯》一书中发现和证明的。该定理内容为：平行四边形的两条对角线所构成的乘积等于对角线的和的平方。

托勒密定理的证明

托勒密定理的证明虽然基于几何形状，但是可以非常简单地用代数法进行证明，不过这里我们不再赘述，感兴趣的读者可以去参考相关数学教材。在几何方法方面，托勒密证明采用了割圆术，其主要的证明方法是通过构造外接圆将一个四边形转化为两个三角形进行证明。

托勒密定理的应用

托勒密定理在实际应用中拥有广泛的运用，尤其在工程中。一些与地图学相关的应用，如GPS等计算地球表面上的距离，都是依据托勒密定理进行的。此外，托勒密定理在图形测量和计算中也有很大的作用。

托勒密定理还被应用于著名的费马点问题中。费马点问题是指寻找给定平面上若干点的位置，使这些点到这些点所形成的三角形三个顶点的距离之和最小。费马点一般用F表示。测地线算法中的贝塞尔实用解法就是采用了托勒密定理，将一个球面三角形所对应的面元在球面上展开成一个六边形，然后通过解六个三角形来求解。

结论

总之，托勒密定理是一条十分重要的定理，在实际应用中也得到了广泛的应用。无论是在基础数学知识学习中，还是在实际应用中，托勒密定理都有着不可取代的作用。