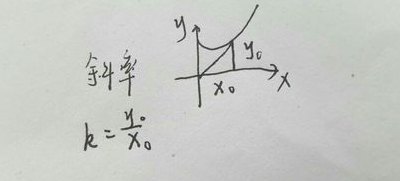斜率是什么(斜率是什么斜率的概念)

斜率是什么

在数学中，斜率是描述两个变量之间关系的概念，通常用于衡量一条直线的陡峭程度或者是变化率。斜率可以用来表示一个变量对另一个变量的响应程度，也可以用来解释两个变量之间的因果关系。在几何学、物理学和经济学等领域，斜率都有着重要的应用。

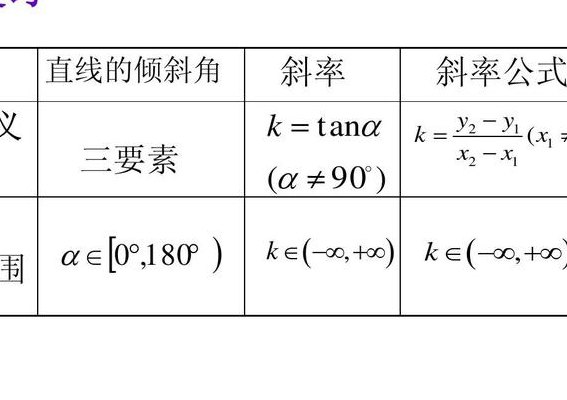
一般来说，斜率是指直线的斜率，即直线上的任意两点之间的垂直距离与水平距离的比值。斜率可以用一个简单的数学公式来表示，即“斜率m等于（y2-y1）除以（x2-x1）”，其中（x1，y1）和（x2，y2）代表直线上的两个点的坐标。这个公式可以帮助我们计算出直线的斜率，从而帮助我们更好地理解直线的走势和变化。

斜率的意义

斜率在数学中具有重要的意义，它不仅可以帮助我们理解直线的特性，还可以用来解决很多实际问题。在几何学中，斜率可以用来描述两条直线的相对陡峭程度，帮助我们比较它们的走势。在物理学中，斜率常常用来表示某种物理量随着时间或位置的变化率，例如速度、加速度等。在经济学中，斜率可以用来衡量供求关系、价格变化、市场走势等。

斜率的应用

斜率在现实生活中有着广泛的应用，它可以帮助我们更好地理解和解决很多与变化率相关的问题。比如，在地理学中，我们可以利用斜率来描述地形的陡峭程度，帮助规划道路、建筑和农田。在经济学中，我们可以利用斜率来分析市场走势，预测价格变化，制定营销策略。在工程学中，我们可以利用斜率来设计坡道、管道和排水系统。

此外，斜率还可以用来解决一些实际问题，比如求解两点之间的最短路径、计算物体的速度、分析时间序列数据等。在科学研究和工程实践中，斜率是一个十分重要的工具，它能够帮助我们更好地理解自然规律和人类活动。

结语

斜率是一个重要的数学概念，它不仅在数学中有着深远的意义，还在物理学、经济学、工程学等领域有着广泛的应用。通过理解斜率的概念和使用斜率的方法，我们可以更好地描述和解释变化率、走势、响应程度等问题。希望本文能够帮助读者更好地理解斜率的概念和应用，并在实际问题中更好地运用斜率。