幂函数公式(幂函数重拾数学之美)

幂函数公式：重拾数学之美

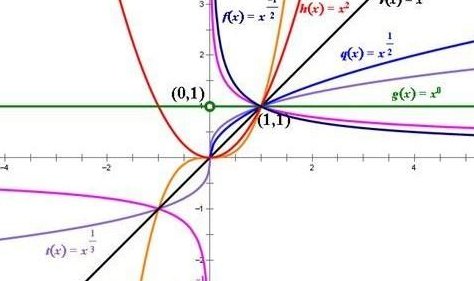
幂函数作为数学中的重要概念，其美妙的表达形式和广泛的应用让人着迷。从古至今，幂函数一直在数学和物理科学中发挥着重要作用。本文将介绍幂函数的基本形式、性质和应用，带您一起探索幂函数背后的数学之美。

基本形式

幂函数的一般形式可以写作 y = x^n，其中 x 为自变量，n 为指数，y 为因变量。当指数 n 为正整数时，这样的函数呈现出典型的“幂律”形式，即随着自变量 x 增大，因变量 y 增加的速度呈指数增长。当指数为负整数时，函数呈现出衰减的趋势，而当指数为零时，则得到常数函数。幂函数的基本形式简洁而优美，正是这种简单性使得幂函数在数学中扮演着重要的角色。

性质

幂函数具有许多重要的性质，使得它成为数学中的重要工具之一。其中最显著的特点之一就是其导数的简单性。对于 y = x^n 这样的幂函数，它的导数很容易计算，即 n * x^(n-1)。这种简单的导数形式使得幂函数在微积分中的应用变得更加便利。此外，幂函数还具有对数性质、指数性质等多种性质，这些性质使得幂函数具有丰富的变化形式，可以描述许多现实世界中的现象。

应用

幂函数在自然科学、工程技术和经济学等领域有着广泛的应用。在物理学中，许多自然规律可以用幂函数来描述，例如牛顿力学中的万有引力定律、光强度随距离的变化规律等。在工程技术中，幂函数被广泛应用于模型拟合、信号处理和系统建模等领域。在经济学中，幂函数也可以用来描述一些特定的经济现象，如价格与需求量之间的关系等。因此，幂函数作为数学中的重要工具，其应用领域非常广泛。

综上所述，幂函数作为数学中的经典概念，其美妙的形式、丰富的性质和广泛的应用使得其成为数学中的瑰宝。通过学习和理解幂函数的基本形式和性质，我们可以更好地理解自然和现实世界中的现象，并且应用幂函数来解决实际问题。因此，幂函数不仅仅是一种数学工具，更是一种展现数学之美的载体。