0是有理数（0是有理数还是无理数）

0是有理数还是无理数

是有理数。0是介于-1和1之间的整数，既是最小的自然数，也是有理数；通常我们把能够写成分数形式称为有理数，不是有理数的实数称为无理数。命名由来 “有理数”这一名称不免叫人费解，有理数并不比别的数更“有道理”。事实上，这似乎是一个翻译上的失误。

是有理数，不是无理数。有理数是整数，和分数的统称，是整数和分数的集合。无理数的定义是无限不循环小数，而0是介于-1和1之间的整数，因此属于有理数。0是介于-1和1之间的整数，是最小的自然数，也是有理数。0不是正数，负数，质数，合数，0是自然数，而是正数和负数的分界点。

有理数是正整数、0、负整数和分数的统称，因此0是有理数。有理数是数学这一科学中对数字的一种概念和定义，有理数是整数与分数这两类数字所构成的集合的一种统称，正整数、负整数、0和分数都是有理数。0是有理数，不是无理数。0是介于-1和1之间的整数。

0是有理数吗

1、是的，0 是有理数。有理数是整数和分数的统称，而整数包括正整数、0、负整数。因此，0 是有理数的一种。在数学中，有理数集可以用大写黑正体符号 Q 代表，但 Q 并不表示有理数，而是表示整个有理数集。有理数集是元素为全体有理数的集合，而有理数则是有理数集中的所有元素。

2、是有理数。0是介于-1和1之间的整数。是最小的自然数，也是有理数。0既不是正数也不是负数，而是正数和负数的分界点。0没有倒数，0的相反数是0，0的绝对值是0，0的平方根是0，0的立方根是0，0乘任何数都等于0，除0之外任何数的0次方等于1。0不能作为分母出现，0的所有倍数都是0。

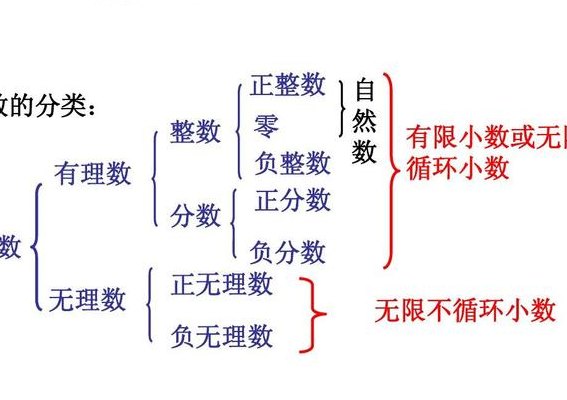
3、正负整数)，有限小数(如0.5)，无限循环小数(如1/3)，无理数是无限不循环小数(如圆周率和根号2)。有理数的概念：⑴正整数、0、负整数统称为整数(0和正整数统称为自然数)。⑵正分数和负分数统称为分数。⑶正整数，0，负整数，正分数，负分数都可以写成分数的形式，这样的数称为有理数。

4、是有理数，不是无理数。0是介于-1和1之间的整数。0是最小的自然数，而且0既不是正数也不是负数，0是正数和负数的分界点。并且0没有倒数，0的相反数是0。有理数是整数（正整数、0、负整数）和分数的统称，是整数和分数的集合。整数也可看做是分母为一的分数。

5、是有理数！实数是由 正 有理数、负有 理数 、 0组成 。0既不是正数，也不是负数。

0属于有理数吗?

是的，0 是有理数。有理数是整数和分数的统称，而整数包括正整数、0、负整数。因此，0 是有理数的一种。在数学中，有理数集可以用大写黑正体符号 Q 代表，但 Q 并不表示有理数，而是表示整个有理数集。有理数集是元素为全体有理数的集合，而有理数则是有理数集中的所有元素。

是有理数。0是介于-1和1之间的整数，既是最小的自然数，也是有理数；通常我们把能够写成分数形式称为有理数，不是有理数的实数称为无理数。命名由来 “有理数”这一名称不免叫人费解，有理数并不比别的数更“有道理”。事实上，这似乎是一个翻译上的失误。

有理数是：整数(包括0，正负整数)，有限小数(如0.5)，无限循环小数(如1/3)，无理数是无限不循环小数(如圆周率和根号2)。有理数的概念：⑴正整数、0、负整数统称为整数(0和正整数统称为自然数)。⑵正分数和负分数统称为分数。

的认识：0是介于-1和1之间的整数。是最小的自然数，也是有理数。0既不是正数也不是负数，而是正数和负数的分界点。0是最小的自然数。0能被任何非零整数整除。0不是奇数，而是偶数（一个非正非负的特殊偶数）。

是有理数，不是无理数。0是介于-1和1之间的整数。0是最小的自然数，而且0既不是正数也不是负数，0是正数和负数的分界点。并且0没有倒数，0的相反数是0。有理数是整数（正整数、0、负整数）和分数的统称，是整数和分数的集合。整数也可看做是分母为一的分数。

0是有理数吗为什么?

是的，0 是有理数。有理数是整数和分数的统称，而整数包括正整数、0、负整数。因此，0 是有理数的一种。在数学中，有理数集可以用大写黑正体符号 Q 代表，但 Q 并不表示有理数，而是表示整个有理数集。有理数集是元素为全体有理数的集合，而有理数则是有理数集中的所有元素。

是有理数。因为有理数的定义是：整数或有限小数或无限循环小数统称为有理数。0是整数，所以0是有理数。供参考，请笑纳。注意：0也是偶数。

是有理数。0是介于-1和1之间的整数。是最小的自然数，也是有理数。0既不是正数也不是负数，而是正数和负数的分界点。0没有倒数，0的相反数是0，0的绝对值是0，0的平方根是0，0的立方根是0，0乘任何数都等于0，除0之外任何数的0次方等于1。0不能作为分母出现，0的所有倍数都是0。

是有理数。0是介于-1和1之间的整数，是最小的自然数，也是有理数。0既不是正数也不是负数，而是正数和负数的分界点。0没有倒数，0的相反数是0，0的绝对值是0，0的平方根是0，0的立方根是0，0乘任何数都等于0，除0之外任何数的0次方等于1。

是一个有理数。0满足有理数的定义，它可以被写作两个整数的比值，并且可以通过整数运算或图像来解释和证明。我们可以将0表示为两个整数的比值，即0/1。根据有理数的定义，分母不能为0，但在这里，我们可以将分子为0，分母为1，得到0/1，也就是0。

0属于有理数还是无理数

是有理数。0是介于-1和1之间的整数，既是最小的自然数，也是有理数；通常我们把能够写成分数形式称为有理数，不是有理数的实数称为无理数。命名由来 “有理数”这一名称不免叫人费解，有理数并不比别的数更“有道理”。事实上，这似乎是一个翻译上的失误。

是有理数。0是介于-1和1之间的整数。是最小的自然数，也是有理数。0既不是正数也不是负数，而是正数和负数的分界点。0没有倒数，0的相反数是0，0的绝对值是0，0的平方根是0，0的立方根是0，0乘任何数都等于0，除0之外任何数的0次方等于1。0不能作为分母出现，0的所有倍数都是0。

是有理数，不是无理数。0是介于-1和1之间的整数。0是最小的自然数，而且0既不是正数也不是负数，0是正数和负数的分界点。并且0没有倒数，0的相反数是0。有理数是整数（正整数、0、负整数）和分数的统称，是整数和分数的集合。整数也可看做是分母为一的分数。

是有理数，不是无理数，无理数也称为无限不循环小数，不能写作两整数之比。若将它写成小数形式，小数点之后的数字有无限多个，并且不会循环，所以0是有理数。常见的无理数有非完全平方数的平方根、π和e，无理数的另一特征是无限的连分数表达式。无理数较早由毕达哥拉斯学派弟子希伯索斯发现。