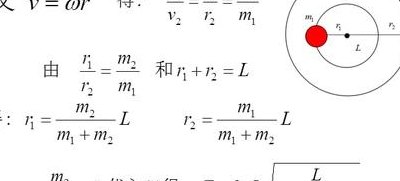双星系统公式及规律（双星系统原理）

双星系统公式推导有哪些?

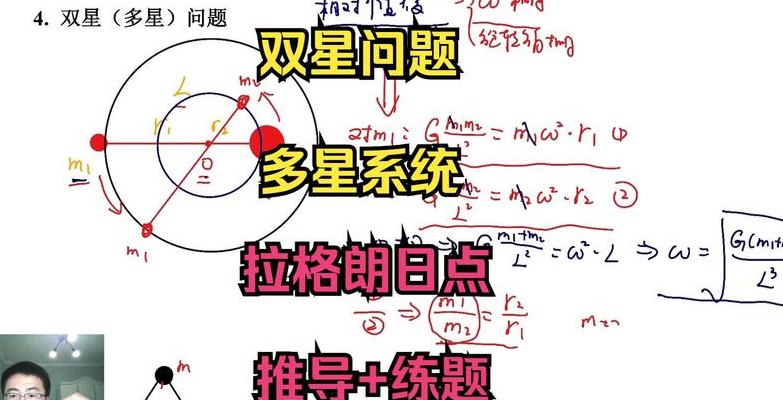
1、双星系统公式总结：T=2πL根号（R/Gm）、T=2πL根号（r/GM）、T=2π根号（L^3/G（M+m））。双星系统是指由两颗恒星组成，相对于其他恒星来说，位置看起来非常靠近的天体系统。联星是指两颗恒星各自在轨道上环绕着共同质量中心的恒星系统。

2、结论：双星运动的周期公式是通过对双星绕固定点转动时的物理规律进行推导得出的。该公式基于牛顿万有引力定律和角动量守恒原理。以下是推导过程的简要概述：双星系统中，每个星体的运动周期相等，这是由万有引力定律Gm1m2/L^2与星体运动的关系决定的。

3、双星问题公式：T=2πL根号（R/Gm）、T=2πL根号（r/GM），T=2π根号（L^3/G（M+m））。

4、双星体系，利用的是角速度相同，意味着周期相同，质量的求解公式，如果周期知道的话，利用万有引力与时间的关系就很容易导出最后的答案，另外利用角速度相等这一条件，通过万有引力与角度的关系利用双星体系间万有引力相等，可以推导出双向体系间质量和半径成反比即r1m1等于r2m2的关系。

物理中的双星系统有哪些公式

1、双星系统公式总结是T=2πL根号（R/Gm）、T=2πL根号（r/GM）、T=2π根号（L^3/G（M+m））。双星系统是指由两颗恒星组成，相对于其他恒星来说，位置看起来非常靠近的天体系统。公式阐述：公式在数学中是指用数学符号或文字表示各个数量之间的关系的式子，具有普遍性，适合于同类关系的所有问题。

2、双星系统公式总结：T=2πL根号（R/Gm）、T=2πL根号（r/GM）、T=2π根号（L^3/G（M+m））。双星系统是指由两颗恒星组成，相对于其他恒星来说，位置看起来非常靠近的天体系统。联星是指两颗恒星各自在轨道上环绕着共同质量中心的恒星系统。

3、双星角速度和周期相等。双星之间的距离：l=r1+r2 万有引力提供它们做圆周运动的向心力，所以它们的向心力也相等。就可以用角速度向心力公式计算得到一些结论。根据3的等式可以得到，双星的运动半径与质量成反比，线速度与质量成反比，向心加速度也与质量成反比。

4、T=2πL根号（R/Gm）、T=2πL根号（r/GM），T=2π根号（L^3/G(M+m)）。已知中心距离为L，运动周期T求总质量，设点O转，R1+R2=L，GMm/L^2=m（2π/T)^2R1，GMm/L^2=m（2π/T)^2R2，两式相加即可。

5、在物理学中，双星系统是一个独特而引人入胜的现象。当我们观察到行星围绕恒星或卫星绕行星的运动时，它们的周期T可以通过万有引力定律计算，T=2πL√(R/Gm) 或 T=2πL√(r/GM)。然而，在双星系统中，情况有所不同。

6、解：设双星系统两星球的质量分别为mm2，其轨道半径分别为RR2，R1+R2=L。

双星系统公式总结是什么?

1、双星系统公式总结是T=2πL根号（R/Gm）、T=2πL根号（r/GM）、T=2π根号（L^3/G（M+m））。双星系统是指由两颗恒星组成，相对于其他恒星来说，位置看起来非常靠近的天体系统。公式阐述：公式在数学中是指用数学符号或文字表示各个数量之间的关系的式子，具有普遍性，适合于同类关系的所有问题。

2、双星系统公式总结：T=2πL根号（R/Gm）、T=2πL根号（r/GM）、T=2π根号（L^3/G（M+m））。双星系统是指由两颗恒星组成，相对于其他恒星来说，位置看起来非常靠近的天体系统。联星是指两颗恒星各自在轨道上环绕着共同质量中心的恒星系统。

3、T=2πL根号（R/Gm）、T=2πL根号（r/GM），T=2π根号（L^3/G(M+m)）。已知中心距离为L，运动周期T求总质量，设点O转，R1+R2=L，GMm/L^2=m（2π/T)^2R1，GMm/L^2=m（2π/T)^2R2，两式相加即可。

4、T=2πL根号（R/Gm）、T=2πL根号（r/GM），T=2π根号（L^3/G（M+m））。

5、双星系统周期公式 ：选其中一星为参考系，另一星仍做匀速圆周运动，折合质量为Mm/(M+m)，由向心力公式GMm/L^2=[Mm/(M+m)][(2派/T)^2]L即可解得T=2派L{L/[G(M+m)]}^0.5。

6、解：设双星系统两星球的质量分别为mm2，其轨道半径分别为RR2，R1+R2=L。

双星系统四个公式推导过程是什么?

M1*R1=M2*R2 M1+M2=4π^2*L^3/GT^2 双星系统周期公式 ：选其中一星为参考系，另一星仍做匀速圆周运动，折合质量为Mm/(M+m)，由向心力公式GMm/L^2=[Mm/(M+m)][(2派/T)^2]L即可解得T=2派L{L/[G(M+m)]}^0.5。

双星运动绕固定点转动，周期相等根据Gm1m2/L^2=m1*4π^2r1/T^2Gm1m2/L^2=m2*4π^2r2/T^2 r1=Gm2T^2/4π^2L^2r2=Gm1T^2/4π^2l^2r1+r2=L m1+m2=4π^2L^3/GT^2 拓展：事物在运动、变化过程中，某些特征多次重复出现，其连续两次出现所经过的时间叫周期。

双星系统公式总结：T=2πL根号（R/Gm）、T=2πL根号（r/GM）、T=2π根号（L^3/G（M+m））。双星系统是指由两颗恒星组成，相对于其他恒星来说，位置看起来非常靠近的天体系统。联星是指两颗恒星各自在轨道上环绕着共同质量中心的恒星系统。

双星系统中,角速度,线速度,质量,轨道半径,向心力都有什么关系?

1、由于力的作用是相互的，所以两子星做圆周运动的向心力大小是相等的，利用万有引力定律可以求得其大小，两子星绕着连线上的一点做圆周运动，所以它们的运动周期是相等的，角速度也是相等的，所以线速度与两子星的轨道半径成正比。

2、。相互间的万有引力是二者各自的向心力 2。

3、圆周运动的半径之比与质量成反比为1：7 双星系统，所以角速度为1：1 线速度之比与半径之比相同 1：7 向心力之比为1：1，两者的向心力为一对作用力与反作用力。

4、在双星系统中，两个星是以它们连线上某一点为圆心，做同角速度的匀速圆周运动，它们间的万有引力提供为所需的向心力。即每个星所需的向心力大小相等，由向心力公式可得 F1向＝F2向 即　m1*ω^2* r1＝m2*ω^2 * r2 所以　m1* r1＝m2* r2 r1 和 r2 分别是它们的圆周半径。

5、双星模型特点： 两颗行星做均速圆周运动所需要的向心力是由它们之间的万有引力提供的，故两星是做均速圆周运动的且向心力大小相等。 两星均绕它们连线上一点做均速圆周运动，因此它们的运行周期和角速度是相等的。 两星做均速圆周运动的半径R1和R2与两星间距L的大小关系：R1+R2=L。