勾股定理证明方法（勾股定理证明方法梅文鼎）

勾股定理的证明方法

几何法：通过构造直角三角形并应用勾股定理来确定斜边长度。代数法：将直角三角形的边长代入勾股定理公式，以证明等式的正确性。数学归纳法：首先验证当直角三角形的斜边长度为某个特定值n时，勾股定理成立，然后展示当斜边长度为n+1时，该定理同样成立。

勾股定理的四种证明方法如下：几何方法：几何方法是最简单的证明方法之一，它是根据几何原理，从绘制三角形特点出发，推导出勾股定理。通过绘制直角三角形，利用几何关系和性质，可以得出a^2 + b^2 = c^2的结论。

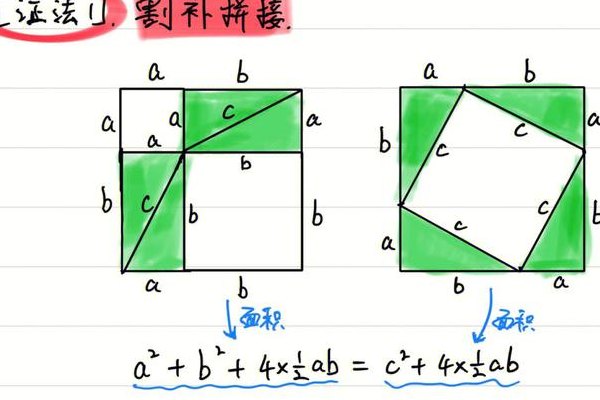
正方形面积法 这是一种很常见的证明方法，具体使用的是面积来证明的。以三角形的三边分别作三个正方形，发现两个较小的正方形面积之和等于较大的那个三角形。勾股定理得到证明。赵爽弦图 赵爽弦图是指用四个斜边长为c，较长直角边为a，较短直角边为c的指教三角形组成一个正方形。

十种方法证明勾股定理

1、几何法：构造一个直角三角形，利用勾股定理求出斜边长。代数法：将直角三角形三边的长度带入勾股定理的公式中，证明等式成立。数学归纳法：证明当斜边长为n时，勾股定理成立，再证明当斜边长为n+1时，勾股定理仍然成立。三角函数法：利用正弦、余弦、正切等三角函数的定义，证明勾股定理。

2、验证勾股定理的十种方法如下：欧拉定理证明法：构造出一个直角三角形，把它的两条直角边对应的两个正方形放在直角三角形外面，另一条边对应的正方形放在直角三角形内部，再利用欧拉定理计算出三个正方形的面积，可以证明勾股定理。

3、毕达哥拉斯证明法 这是勾股定理的最早证明之一，由古希腊数学家毕达哥拉斯给出。证明的方法是通过构造一个直角三角形，并利用三角形的面积公式来证明。欧几里得证明法 欧几里得是古希腊数学家，他的《几何原本》是世界上最早的公理化数学著作。在书中，欧几里得给出了勾股定理的一个简单证明。

4、勾股定理的最简单的十种证明方法的回答如下：方法一：利用余弦定理证明勾股定理。设三角形ABC的三个边分别为a、b、c，且角C为90度。根据余弦定理：c^2=a^2+b^2-2abcosC。因为角C等于90度，所以cosC等于0。所以c^2=a^2+b^2。

5、采用的是割补法： 如图，将图中的四个直角三角形涂上朱色，把中间小正方形涂上黄色，叫做中黄实，以弦为边的正方形称为弦实，然后经过拼补搭配，“令出入相补，各从其类”，他肯定了勾股弦三者的关系是符合勾股定理的。即“勾股各自乘，并之为弦实，开方除之，即弦也”。

证明勾股定理最简单的十种方法

验证勾股定理的十种方法如下：欧拉定理证明法：构造出一个直角三角形，把它的两条直角边对应的两个正方形放在直角三角形外面，另一条边对应的正方形放在直角三角形内部，再利用欧拉定理计算出三个正方形的面积，可以证明勾股定理。

几何法：构造一个直角三角形，利用勾股定理求出斜边长。代数法：将直角三角形三边的长度带入勾股定理的公式中，证明等式成立。数学归纳法：证明当斜边长为n时，勾股定理成立，再证明当斜边长为n+1时，勾股定理仍然成立。三角函数法：利用正弦、余弦、正切等三角函数的定义，证明勾股定理。

邹元治证明法 这是中国清代数学家邹元治的一种证明方法。他利用了三角形面积的另一种计算方法来证明勾股定理。帕斯卡证明法 帕斯卡是法国数学家和物理学家，他通过巧妙地利用三角形面积公式，证明了勾股定理。雷登证明法 雷登是荷兰数学家，他利用了三角形的相似性质来证明勾股定理。