两直线垂直斜率关系(两直线垂直斜率关系如何证明)
两条直线垂直,斜率有什么关系?
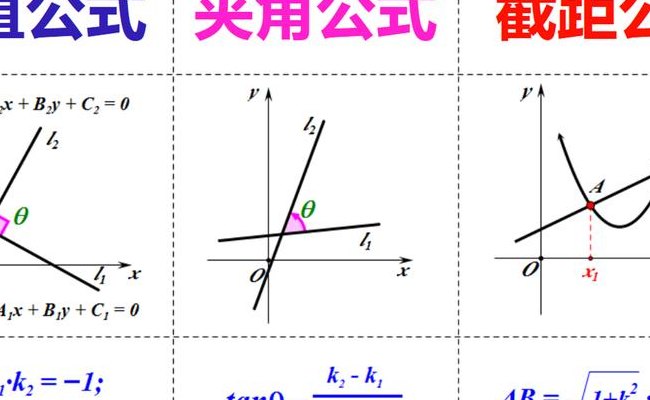
如果两条直线的斜率都存在。则,它们的斜率之积=-1。如果其中一条直线的斜率不存在。则,另一条直线的斜率=0。如果直线与x轴垂直,直角的正切值无穷大,故此直线不存在斜率。 当直线L的斜率存在时,对于一次函数y=kx+b(斜截式),k即该函数图像(直线)的斜率。
垂直的直线斜率的关系如下:两条垂直相交直线的斜率相乘积为-1。斜率是表示一条直线(或曲线的切线)关于(横)坐标轴倾斜程度的量。它通常用直线(或曲线的切线)与(横)坐标轴夹角的正切,或两点的纵坐标之差与横坐标之差的比来表示。
两直线垂直,在两者斜率都存在的前提下,其斜率的乘积为-1;如果其中直线不存在斜率,则另一条直线斜率为0。对于两条互相垂直的直线而言,它们的斜率互为倒数,因此其斜率的乘积为-1。斜率是什么 斜率指的是一条直线或是曲线的切线与横坐标轴倾斜程度的量。
两条直线平行,斜率相等,两条直线垂直,二者斜率相乘就为-1。两条直线的斜率相等是两条直线平行的充分条件,即:如果两条直线的斜率相等,那么这两条直线一定平行。两条直线都平行于y轴时,两直线的斜率都不存在。如果两条直线垂直,那么斜率相乘就为-1。
两直线垂直,那么斜率怎么计算呢?
1、所以1+tanatanb=1+k1k2=0。因此k1k2=-1。方法二:设一条直线的斜率是tana,另一条是tanb,两条线的夹角为b-a。tan(b-a)=[tanb-tana]/[1+tana tanb]。如果 1 + tana tanb = 0,即 tana tanb = -1。那么 b - a = 90度。
2、斜率计算:ax+by+c=0中,k=-a/b,直线斜率公式:k=(y2-y1)/(x2-x1),两条垂直相交直线的斜率相乘积为-1,k1*k2=-1。
3、先设直线LL2的方程分别为:L1=k1X+b1,L2=K2X+b2(k1,k2分别是直线LL2的斜率)倾斜角分别为α ,θ(α >θ)。
4、两条直线平行,斜率相等,两条直线垂直,二者斜率相乘就为-1。两条直线的斜率相等是两条直线平行的充分条件, 即:如果两条直线的斜率相等,那么这两条直线一定平行。两条直线都平行于y轴时,两直线的斜率都不存在。如果两条直线垂直,那么斜率相乘就为-1。
两直线垂直斜率关系是什么?
如果两条直线的斜率都存在。则,它们的斜率之积=-1。如果其中一条直线的斜率不存在。则,另一条直线的斜率=0。如果直线与x轴垂直,直角的正切值无穷大,故此直线不存在斜率。当直线L的斜率存在时,对于一次函数y=kx+b(斜截式),k即该函数图像(直线)的斜率。
两条互相垂直的直线的斜率具有以下关系:它们的斜率之积为-1。也就是说,一条直线的斜率如果是m,另一条与之垂直的直线的斜率则为-1/m。下面将对这一现象进行详细解释。垂直直线的定义与性质 在数学中,当两条直线相交且形成的角度恰好为直角时,我们称这两条直线是垂直的。
两直线垂直,在两者斜率都存在的前提下,其斜率的乘积为-1;如果其中直线不存在斜率,则另一条直线斜率为0。对于两条互相垂直的直线而言,它们的斜率互为倒数,因此其斜率的乘积为-1。斜率是什么 斜率指的是一条直线或是曲线的切线与横坐标轴倾斜程度的量。
两条直线垂直它们的斜率有什么关系
两条直线垂直时,它们的斜率互为相反数的倒数关系。具体来说,如果一条直线的斜率为m,那么与其垂直的另一条直线的斜率就是-1/m。值得注意的是,若直线斜率不存在,其往往是垂直于x轴的直线,这种情况同样适用于垂直关系的判断。
如果两条直线的斜率都存在。则,它们的斜率之积=-1。如果其中一条直线的斜率不存在。则,另一条直线的斜率=0。如果直线与x轴垂直,直角的正切值无穷大,故此直线不存在斜率。当直线L的斜率存在时,对于一次函数y=kx+b(斜截式),k即该函数图像(直线)的斜率。
垂直的直线斜率的关系如下:两条垂直相交直线的斜率相乘积为-1。斜率是表示一条直线(或曲线的切线)关于(横)坐标轴倾斜程度的量。它通常用直线(或曲线的切线)与(横)坐标轴夹角的正切,或两点的纵坐标之差与横坐标之差的比来表示。
两直线垂直,在两者斜率都存在的前提下,其斜率的乘积为-1;如果其中直线不存在斜率,则另一条直线斜率为0。对于两条互相垂直的直线而言,它们的斜率互为倒数,因此其斜率的乘积为-1。斜率是什么 斜率指的是一条直线或是曲线的切线与横坐标轴倾斜程度的量。
两条互相垂直的直线的斜率具有以下关系:它们的斜率之积为-1。也就是说,一条直线的斜率如果是m,另一条与之垂直的直线的斜率则为-1/m。下面将对这一现象进行详细解释。垂直直线的定义与性质 在数学中,当两条直线相交且形成的角度恰好为直角时,我们称这两条直线是垂直的。
两条互相垂直的直线,其斜率有什么关系?快
两条互相垂直的直线的斜率具有以下关系:它们的斜率之积为-1。也就是说,一条直线的斜率如果是m,另一条与之垂直的直线的斜率则为-1/m。下面将对这一现象进行详细解释。垂直直线的定义与性质 在数学中,当两条直线相交且形成的角度恰好为直角时,我们称这两条直线是垂直的。
当两条直线互相垂直时,它们的斜率关系有一个明确的数学法则。首先,如果一条直线的斜率为0,而另一条直线的斜率不存在(即垂直于x轴),它们之间没有直接的斜率关系。但当两条直线都有斜率时,关键的结论是它们的斜率乘积必须等于-1,即k1 * k2 = -1,这表明它们是互为负倒数关系。
垂直的直线斜率的关系如下:两条垂直相交直线的斜率相乘积为-1。斜率是表示一条直线(或曲线的切线)关于(横)坐标轴倾斜程度的量。它通常用直线(或曲线的切线)与(横)坐标轴夹角的正切,或两点的纵坐标之差与横坐标之差的比来表示。
如果两条直线的斜率都存在。则,它们的斜率之积=-1。如果其中一条直线的斜率不存在。则,另一条直线的斜率=0。如果直线与x轴垂直,直角的正切值无穷大,故此直线不存在斜率。当直线L的斜率存在时,对于一次函数y=kx+b(斜截式),k即该函数图像(直线)的斜率。
两直线垂直,在两者斜率都存在的前提下,其斜率的乘积为-1;如果其中直线不存在斜率,则另一条直线斜率为0。对于两条互相垂直的直线而言,它们的斜率互为倒数,因此其斜率的乘积为-1。斜率是什么 斜率指的是一条直线或是曲线的切线与横坐标轴倾斜程度的量。
两条直线平行,斜率相等,两条直线垂直,二者斜率相乘就为-1。两条直线的斜率相等是两条直线平行的充分条件, 即:如果两条直线的斜率相等,那么这两条直线一定平行。两条直线都平行于y轴时,两直线的斜率都不存在。如果两条直线垂直,那么斜率相乘就为-1。