勾股定理（勾股定理是谁发现的）

勾股定理的定义

1、勾股定理是一种在直角三角形中发现的数学关系，即直角三角形的两条直角边长度的平方和等于斜边长度的平方。这一定理被广泛用于数学、物理和工程领域，是许多重要定理和公式的基础。

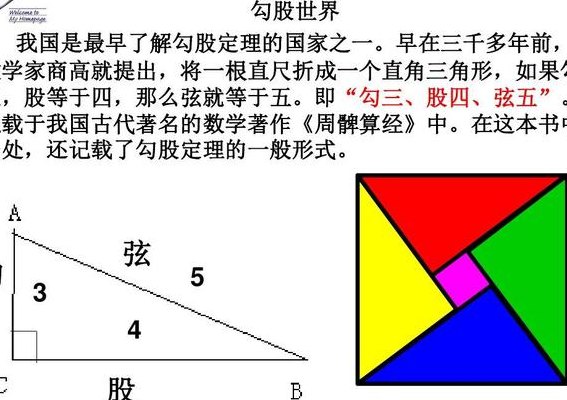
2、勾股定理，是一个基本的几何定理，指直角三角形的两条直角边的平方和等于斜边的平方。中国古代称直角三角形为勾股形，并且直角边中较小者为勾，另一长直角边为股，斜边为弦，所以称这个定理为勾股定理，也有人称商高定理。

3、勾股定理就是 直角 三角形斜边上的正方形面积，等于两直角边上的正方形面积之和。 中国 古代称两直角边为勾和股，斜边为弦。勾三股四弦五就是：勾三的平方九，加股四的平方十六，等于弦五的平方二十五。

4、勾股定理（又称商高定理，毕达哥拉斯定理）是一个基本的几何定理，早在中国商代就由商高发现。据说毕达高拉斯发现了这个定后，即斩了百头牛作庆祝，因此又称“百牛定理”。

勾股定理是什么?

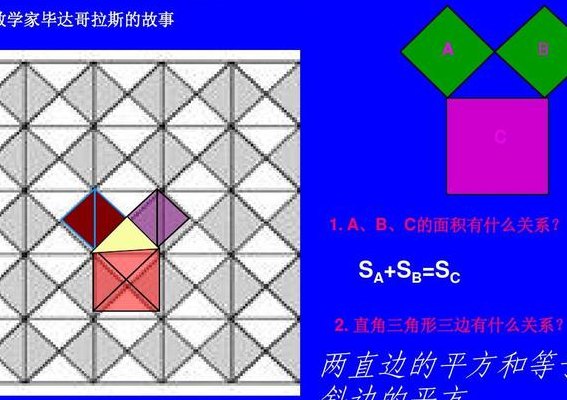
勾股定理是一个著名的几何定理，它描述了直角三角形中三条边的长度之间的关系。这个定理在数学、工程、建筑等领域都有着广泛的应用。勾股定理的内容是：在一个直角三角形中，斜边的平方等于两条直角边的平方和。

勾股定理：在任何一个直角三角形中，两条直角边的平方之和一定等于斜边的平方。这个定理在中国又称为“商高定理”，在外国称为“毕达哥拉斯定理”。

勾股定理： 　　在我国，把直角三角形的两直角边的平方和等于斜边的平方这一特性叫做勾股定理或勾股弦定 古埃及人利用打结作RT三角形理，又称毕达哥拉斯定理或毕氏定理(Pythagoras Theorem)。

勾股定律指：是一个基本的几何定理，指直角三角形的两条直角边的平方和等于斜边的平方。

勾股定理，是一个基本的几何定理，指直角三角形的两条直角边的平方和等于斜边的平方。中国古代称直角三角形为勾股形，并且直角边中较小者为勾，另一长直角边为股，斜边为弦，所以称这个定理为勾股定理，也有人称商高定理。

勾股定理是什么

1、勾股定理是一个关于直角三角形的数学定理。它指出：在直角三角形中，直角边的平方等于斜边的平方减去其中一条非直角边的平方。勾股定理的数学公式为：a^2 + b^2 = c^2 其中，a和b是直角三角形的两条直角边，c是斜边。

2、勾股定理是一个初等几何定理，是人类早期发现并证明的重要数学定理之一，用代数思想解决几何问题的最重要的工具之一，也是数形结合的纽带之一。勾股定理是余弦定理的一个特例。

3、勾股定律指：是一个基本的几何定理，指直角三角形的两条直角边的平方和等于斜边的平方。中国古代称直角三角形为勾股形，并且直角边中较小者为勾，另一长直角边为股，斜边为弦，所以称这个定理为勾股定理，也有人称商高定理。