圆锥的侧面展开图（圆锥的侧面展开图面积公式）

圆锥的侧面展开图是一个什么图形

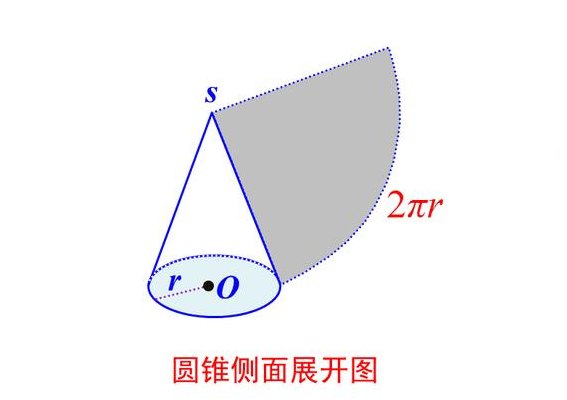
圆锥的侧面展开图为扇形。扇形的半径为圆锥的母线，扇形的弧长为圆锥的底面周长。

圆锥的侧面展开图是扇形。立体几何定义：以直角三角形的直角边所在直线为旋转轴，其余两边旋转360度而成的曲面所围成的几何体叫做圆锥。旋转轴叫做圆锥的轴。垂直于轴的边旋转而成的曲面叫做圆锥的底面。不垂直于轴的边旋转而成的曲面叫做圆锥的侧面。

圆锥的侧面积：将圆锥的侧面沿母线展开，是一个扇形，这个扇形的弧长等于圆锥底面的周长，而扇形的半径等于圆锥的母线的长.圆锥的侧面积就是弧长为圆锥底面的周长×母线/2；没展开时是一个曲面。圆锥有一个底面、一个侧面、一个顶点、一条高、无数条母线，且底面展开图为一圆形，侧面展开图是扇形。

圆锥的侧面展开图是什么图形?

1、圆锥有一个底面、一个侧面、一个顶点、一条高、无数条母线，且底面展开图为一圆形，侧面展开图是扇形。

2、圆锥的侧面展开图是一个扇形，其有关内容如下：定义和性质：圆锥是一种旋转体，由一个直角三角形绕其直角边旋转而成。圆锥的侧面展开图是一个扇形，其中扇形的半径称为圆锥的母线，扇形的弧长称为圆锥的底面周长。扇形面积的计算：扇形的面积可以通过其半径和中心角来计算。

3、圆锥三视图是观测者从三个不同位置观察而画出的图形。圆锥主视图和侧视图均为等腰三角形，俯视图是一个圆和圆心。圆锥有一个底面、一个侧面、一个顶点、一条高、无数条母线，且底面展开图为一圆形，侧面展开图是扇形。

4、圆锥的侧面展开图为扇形。扇形的半径为圆锥的母线，扇形的弧长为圆锥的底面周长。

5、在展开过程中，圆锥的底面圆会变成一个线段，这个线段就是扇形的弧长。因此，当我们把圆锥的侧面展开时，得到的图形是一个扇形。“圆锥”一词用来指代正圆锥，即圆锥顶点在底面的投影是圆心时的情况。如果顶点在底面的投影不在圆心，这样的圆锥则被称为斜圆锥。

6、圆锥的侧面展开图是扇形。详细解释如下：圆锥是一种三维几何体，由一个圆形底面和一个顶点连接而成的表面。当我们考虑其侧面时，它是一个曲面。为了更直观地理解这个曲面，我们可以将其展开成一个平面图形。展开的方式是：从圆锥的顶点开始，沿着侧面的斜边将其剪开并平铺在一个平面上。

圆锥的侧面展开图是什么样的,画图给采纳

1、圆锥的侧面展开图为扇形。扇形的半径为圆锥的母线，扇形的弧长为圆锥的底面周长。

2、圆锥体表面展开图是一个扇形，如下：正圆锥的侧面可以展开为平面上的一个扇形。这个扇形所在的圆半径就是圆锥的斜高，对应的圆弧长为底部圆形的周长。

3、圆锥的展开图形是扇形。将圆锥的侧面沿母线展开，是一个扇形，这个扇形的弧长等于圆锥底面的周长，而扇形的半径等于圆锥的母线的长。圆锥的侧面积就是弧长为圆锥底面的周长×母线／2；没展开时是一个曲面。

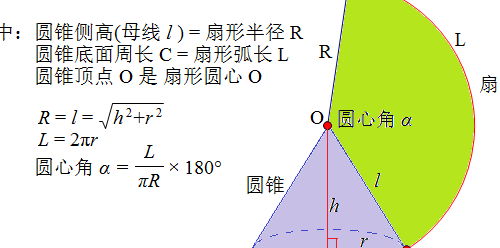
4、圆锥的侧面展开图是扇形 圆锥的几个重要公式：圆锥的高：h=√（l*l-r*r）（l：母线长，r：底面半径）。圆锥的底面周长：C=2*π*r=α*l（r：底面半径，α：侧面展开图圆心角弧度，l：母线长）。圆锥的表面积由侧面积和底面积两部分组成。

5、圆锥的侧面展开是一个扇形，扇形指的是一条圆弧和经过这条圆弧两端的两条半径所围成的图形，是圆的一部分，由两个半径和一段弧围成，在较小的区域被称为小扇形，较大的区域被称为大扇形。

6、圆锥的侧面积：将圆锥的侧面沿母线展开，是一个扇形，这个扇形的弧长等于圆锥底面的周长，而扇形的半径等于圆锥的母线的长.圆锥的侧面积就是弧长为圆锥底面的周长×母线/2；没展开时是一个曲面。圆锥有一个底面、一个侧面、一个顶点、一条高、无数条母线，且底面展开图为一圆形，侧面展开图是扇形。

圆锥的展开图怎么画?

圆锥体表面展开图是一个扇形，如下：正圆锥的侧面可以展开为平面上的一个扇形。这个扇形所在的圆半径就是圆锥的斜高，对应的圆弧长为底部圆形的周长。

画圆锥体的展开图，分3部分，先画出圆锥体的侧面，再画出圆锥体的底，即可完成，具体的画法步骤如下：在一个平面上画上下两点，两点的距离是圆锥体的侧边长。以其中一个点为基础，用圆规从另一点画弧。弧长是圆锥底面周长，并将边弧连接到原点。

CAD画出圆锥的展开图的步骤如下：先定好是多大的圆锥形，如下图所示，我们有一个圆锥，高为50，底部圆形半径为20。

圆锥体展开图由一个扇形（圆锥的侧面）和一个圆（圆锥的底面）组成。

要使用CAD绘制圆锥的展开图，首先确定圆锥的尺寸，比如一个高度为50、底部半径为20的圆锥。步骤如下：开始时，使用圆弧命令，画出一个与圆锥侧面上的斜边等长的弧形，弧形的圆心在圆锥的顶端，形成一个大圆弧。接着，计算圆锥底部圆的周长，周长公式为2πr，代入20的半径，得到126的长度。