向量共线(向量共线方向相同吗)
共线向量是什么啊?有什么公式没?
共线向量是方向相同或相反的向量,存在于同一条直线上。具体公式有:若向量AB与向量CD共线,则存在实数λ,使得向量AB=λ向量CD。或者向量AB与向量CD平行,即方向相同或相反,满足公式向量AB=m向量DC。当向量AB与向量CD方向相反时,λ为负实数。
方向相同或相反的非零向量叫平行向量(equal vector)。表示为a∥b 任意一组平行向量都可移到同一直线上,因此平行向量也叫共线向量(collinear vectors)。规定:0向量与任意向量平行。向量共线的充要条件:若向量a与向量b(b为非零向量)共线,则a=λb(λ为实数)。
共线向量,简单来说,是指在同一个直线上方向相同或相反的非零向量。它们之间的关系可以用符号∥表示,即a∥b,这意味着任意一组平行向量都可以沿着同一条直线移动,因此也被称作共线向量。特别地,0向量与任何非零向量都被认为是平行的。
共线向量也就是平行向量,方向相同或相反的非零向量叫平行向量,表示为a∥b,任意一组平行向量都可移到同一直线上,所以称为共线向量。共线向量也就是平行向量,方向相同或相反的非零向量叫平行向量,表示为a∥b ,任意一组平行向量都可移到同一直线上,所以称为共线向量。
什么是向量共线?
共线向量也就是平行向量,方向相同或相反的非零向量叫平行向量。任意一组平行向量都可移到同一直线上,所以称为共线向量。共线向量基本定理为如果a≠0,那么向量b与a共线的充要条件是:存在实数λ,使得b=λa。数学中,向量,指具有大小和方向的量。它可以形象化地表示为带箭头的线段。
共线向量也就是平行向量,方向相同或相反的非零向量叫平行向量,表示为a∥b,任意一组平行向量都可移到同一直线上,所以称为共线向量。共线向量也就是平行向量,方向相同或相反的非零向量叫平行向量,表示为a∥b ,任意一组平行向量都可移到同一直线上,所以称为共线向量。
意思是两条向量所在的直线不平行也不重合。设向量a,b,a,b不共线即a,b不平行(a,b是自由向量,平行即共线),因平行的条件是存在常数k,使b=ka,故不共线的条件是b=ka不成立,即两向量不成比例。
向量共线是什么意思?怎么证明呢?
共线向量也就是平行向量,方向相同或相反的非零向量叫平行向量,表示为a∥b,任意一组平行向量都可移到同一直线上,所以称为共线向量。共线向量也就是平行向量,方向相同或相反的非零向量叫平行向量,表示为a∥b ,任意一组平行向量都可移到同一直线上,所以称为共线向量。
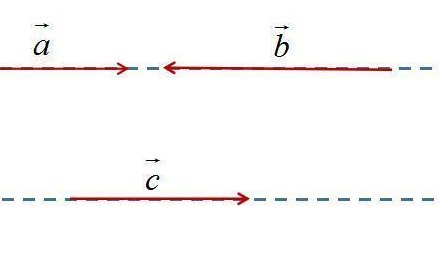
共线向量是指方向相同或相反的向量,它们位于同一条直线上。在几何学中,当我们说两个向量共线时,意味着它们指向的方向是一致的或者相反。例如,想象一条直线上的两个方向箭头,不论它们是正方向还是反方向,只要它们都在同一条直线上,它们就是共线的。
共线向量也就是平行向量,方向相同或相反的非零向量叫平行向量,表示为a∥b ,任意一组平行向量都可移到同一直线上,所以称为共线向量。共线向量基本定理为如果 a≠0,那么向量b与a共线的充要条件是:存在唯一实数λ,使得 b=λa。
向量的共线指的是两个或多个向量的方向相同或相反的关系。换句话说,如果存在一个非零向量c,使得向量a和向量b可以表示为c的倍数,那么向量a和向量b就是共线的。如果向量a和向量b共线,那么可以用一个数k乘以向量a就等于向量b,即a=k*b(k为非零数)。在几何上,共线的向量在同一条直线上。
共线向量指的是在同一直线上的向量。如果两个向量a和b共线,那么它们可以表示为a=k*b的形式,其中k是一个常数。共线向量具有相同的方向或相反的方向,它们的长度可以不相等。共线向量可以在几何学、物理学和线性代数等领域中起到重要的作用。