诱导公式口诀（诱导公式口诀奇变偶不变什么意思）

诱导公式三角函数基本公式

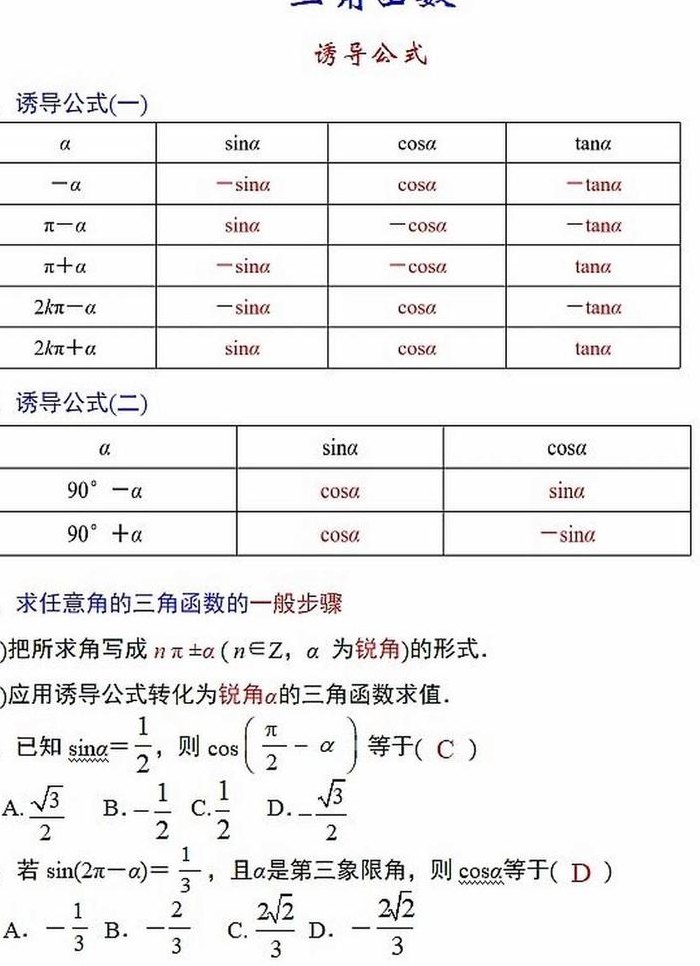
1、三角函数常用诱导公式有： sin(2kπ+a)=sina (k∈Z)、cos(2kπ+a)=cosa (k∈Z)、 tan(2kπ +a )=tana (k∈Z)、cot(2kπ+a)=cota (k∈Z)等。

2、诱导公式三角函数基本公式如下：公式一 设α为任意角，终边相同的角的同一三角函数的值相等：sin（2kπ＋α）＝sinα（k∈Z）；cos（2kπ＋α）＝cosα（k∈Z）；tan（2kπ＋α）＝tanα（k∈Z）；cot（2kπ＋α）＝cotα （k∈Z）。

3、三角诱导函数公式如下：正弦函数的诱导公式：sin（x+2π）=sin（x），sin（x+π）=-sin（x），sin（x+π/2）=cos（x），sin（x-π/2）=-cos（x）。

4、所谓三角函数诱导公式，就是将角n·(π/2)±α的三角函数转化为角α的三角函数。

三角函数的诱导公式有哪些?

1、正弦函数的诱导公式：sin（x+2π）=sin（x），sin（x+π）=-sin（x），sin（x+π/2）=cos（x），sin（x-π/2）=-cos（x）。余弦函数的诱导公式：cos（x+2π）=cos（x），cos（x+π）=-cos（x），cos（x+π/2）=-sin（x）cos（x-π/2）=sin（x）。

2、三角函数常用诱导公式有：sin(2kπ+α)=sinα(k∈Z)、cos(2kπ+α)=cosα(k∈Z)、tan(2kπ+α)=tanα(k∈Z)、cot(2kπ+α)=cotα(k∈Z)等。三角函数诱导公式记忆口诀：“奇变偶不变，符号看象限”。

3、三角函数诱导公式是3π/2+α=sinα/（-cosα）=-tanα直接写成：cot（3π/2+α）=1/tan（3π/2+α）=-tanα。三角函数是基本初等函数之一，是以角度（数学上最常用弧度制，下同）为自变量，角度对应任意角终边与单位圆交点坐标或其比值为因变量的函数。

4、这个公式同样也可以帮助我们计算三角形中的未知边长。正弦函数和余弦函数的诱导公式。sin(x+π/2)=cos(x)cos(x+π/2)=-sin(X)这两个公式表明，正弦函数和余弦函数之间存在一种特殊的关系，即它们的相位差为π/2。这个公式在计算三角函数的复合函数时非常有用。

诱导公式的口诀是什么?

1、诱导公式口诀如下：诱导公式记忆口诀：“奇变偶不变，符号看象限”。“奇、偶”指的是r/2的倍数的奇偶，变与不变”指的是三角函数的名称的变化：变”是指正弦变余弦，正切变余切。

2、诱导公式记忆口诀：“奇变偶不变，符号看象限”。诱导公式是数学三角函数中将角度比较大的三角函数利用角的周期性，转换为角度比较小的三角函数。在四个象限的符号如何判断，也可以记住口诀“一全正；二正弦(余割)；三两切；四余弦(正割)”。

3、各种三角函数在四个象限的符号如何判断，也可以记住口诀：一全正；二正弦；三两切；四余弦。诱导公式：公式一：终边相同的角的同一三角函数的值相等。

诱导公式的口诀是?

1、诱导公式口诀如下：诱导公式记忆口诀：“奇变偶不变，符号看象限”。“奇、偶”指的是r/2的倍数的奇偶，变与不变”指的是三角函数的名称的变化：变”是指正弦变余弦，正切变余切。

2、诱导公式记忆口诀：“奇变偶不变，符号看象限”。诱导公式是数学三角函数中将角度比较大的三角函数利用角的周期性，转换为角度比较小的三角函数。在四个象限的符号如何判断，也可以记住口诀“一全正；二正弦(余割)；三两切；四余弦(正割)”。

3、各种三角函数在四个象限的符号如何判断，也可以记住口诀：一全正；二正弦；三两切；四余弦。诱导公式：公式一：终边相同的角的同一三角函数的值相等。

诱导公式

1、诱导公式：(kπ)/2±α，其中k为奇数时，正弦变余弦，余弦变正弦，正切变余切，余切变正切；符号看象限。k为偶数时，函数名称不变。简记为：奇变偶不变，符号看象限。两角和与差公式：关键是要记住cos(α-β)=cosαcosβ+sinαsinβ。

2、高一诱导公式六个如下：公式一：sin（2kπ＋α）＝sinα（k∈Z）。cos（2kπ＋α）＝cosα（k∈Z）。tan（2kπ＋α）＝tanα（k∈Z）。公式二：sin（π＋α）＝－sinα。cos（π＋α）＝－cosα。tan（π＋α）＝tanα。公式三：sin（－α）＝－sinα。cos（－α）＝cosα。

3、正弦函数的诱导公式。sin(-x)=-sin(X)这个公式表明，正弦函数的值在x轴上是关于原点对称的。也就是说，如果一个角度的正弦值为a，那么它的相反数的正弦值就是-a，这个公式在解决一角形问题时非常有用，因为它可以帮助我们计算负角度的正弦值。余弦函数的诱导公式。

4、诱导公式是指三角函数中将角度比较大的三角函数利用角的周期性，转换为角度比较小的三角函数的公式。诱导公式有六组共54个。

5、八个诱导公式是什么：sin(2kπ+α)=sinα(k∈Z)、cos(2kπ+α)=cosα(k∈Z)、tan(2kπ+α)=tanα(k∈Z)、cot(2kπ+α)=cotα(k∈Z)。数学诱导公式 数学诱导公式是三角函数，利用周期性将角度比较大的三角函数，转换为角度比较小的三角函数的公式。诱导公式有六组，共54个。

6、三角函数诱导公式（Induction formula)是一种数学公式，就是将任意角的三角函数转化为锐角的三角函数。包括一些常用的公式和和差化积公式。万能公式推导：sin2α＝2sinαcosα＝2sinαcosα／。（因为cos(α）＋sin(α）＝1)。再把分式上下同除cos^2(α），可得sin2α＝2tanα／。