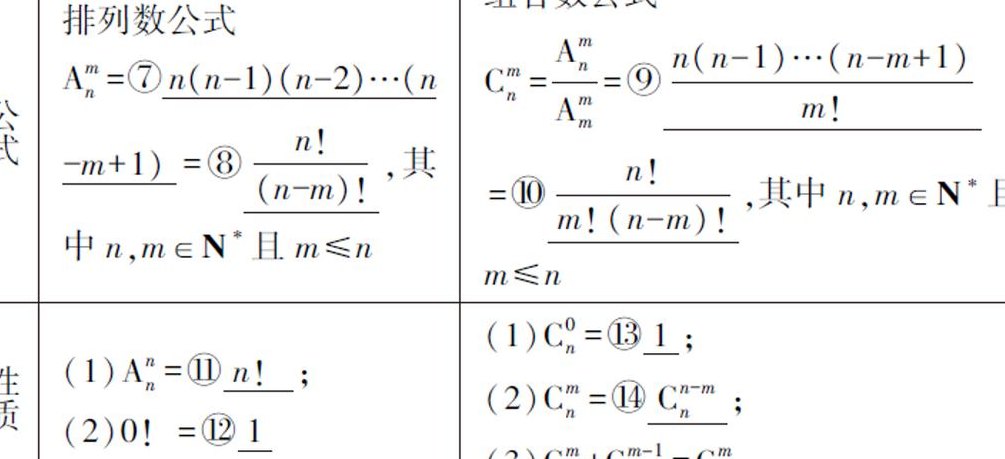排列组合的公式(排列组合的公式和方法)
排列组合的公式
1、排列组合的计算公式如下:排列的计算公式:P = n! / !,其中n表示总的元素数量,r表示需要排列的元素数量,“!”表示阶乘。组合的计算公式:C = n! / [r!],或者更简洁地表示为 C = P / r!。其中各项含义与排列公式相同。
2、排列组合的计算公式是A(n,m)=n×(n-1).(n-m+1)=n/(n-m)。排列组合是组合学最基本的概念,所谓排列,就是指从给定个数的元素中取出指定个数的元素进行排序,组合则是指从给定个数的元素中仅仅取出指定个数的元素,不考虑排序。
3、计算公式:;C(n,m)=C(n,n-m)。(n≥m)C-Combination 组合数 ;A-Arrangement 排列数(在旧教材为P-Permutation);N-Number 元素的总个数;M- 参与选择的元素个数;!- Factorial阶乘。
4、排列组合的计算公式为:排列数公式A(n,m)=n!/(n-m)!,组合数公式C(n,m)=n!/[m!(n-m)!]。排列,是指从n个不同元素中,任取m(m≤n)个元素按照一定的顺序排成一列。排列数公式A(n,m)表示的是从n个不同元素中取出m个元素的所有排列的个数。
排列组合的计算公式是什么?
1、排列组合的计算公式是A(n,m)=n×(n-1).(n-m+1)=n/(n-m)。排列组合是组合学最基本的概念,所谓排列,就是指从给定个数的元素中取出指定个数的元素进行排序,组合则是指从给定个数的元素中仅仅取出指定个数的元素,不考虑排序。
2、排列组合计算公式如下:从n个不同元素中取出m(m≤n)个元素的所有排列的个数,叫做从n个不同元素中取出m个元素的排列数,用符号 A(n,m)表示。
3、排列组合计算公式如下:排列数:从n个中取m个排一下,有n(n-1)(n-2)……(n-m+1)种,即n!/(n-m)!组合数:从n个中取m个,相当于不排,就是n!/[(n-m)!m!]。
4、计算公式是:A(n,m)=n(n-1)(n-2)?(n-m+1)=n!/(n-m)!此外规定0!=1,n!表示n(n-1)(n-2)?1 例如:6!=6x5x4x3x2x1=720,4!=4x3x2x1=24。(2)组合数公式 组合用符号C(n,m)表示,m_n。公式是:C(n,m)=A(n,m)/m! 或 C(n,m)=C(n,n-m)。
5、计算公式:;C(n,m)=C(n,n-m)。(n≥m)C-Combination 组合数 ;A-Arrangement 排列数(在旧教材为P-Permutation);N-Number 元素的总个数;M- 参与选择的元素个数;!- Factorial阶乘。
6、排列组合计算公式?排列组合计算公示:C(n,m)=C(n,n-m)。(n≥m)排列组合基本介绍:排列组合是组合学最基本的概念。所谓排列,就是指从给定个数的元素中取出指定个数的元素进行排序。组合则是指从给定个数的元素中仅仅取出指定个数的元素,不考虑排序。
什么叫排列组合?它的公式是什么?
1、排列组合的计算公式是A(n,m)=n×(n-1).(n-m+1)=n/(n-m)。排列组合是组合学最基本的概念,所谓排列,就是指从给定个数的元素中取出指定个数的元素进行排序,组合则是指从给定个数的元素中仅仅取出指定个数的元素,不考虑排序。
2、排列组合是数学中的一个重要概念,它用于描述从一组元素中选取若干个元素的不同方式。排列和组合是两个不同的概念,它们的区别在于是否考虑元素的顺序。排列是指从n个元素中选取r个元素,并且考虑元素的顺序。
3、排列组合计算公式如下:从n个不同元素中取出m(m≤n)个元素的所有排列的个数,叫做从n个不同元素中取出m个元素的排列数,用符号 A(n,m)表示。
排列组合问题怎么做?
要使至少两个发生所以可以考虑为恰有两个发生与三个都发生的可能情况之和,故第一问按照排列组合公式表达为 C(2,3)+C(3,3)=3*2/(2*1)+3*2*1/(3*2*1)=4 (其中括号内第一个数字为上标,第二个数字为下标)。
相邻问题捆绑法:题目中规定相邻的几个元素捆绑成一个组,当作一个大元素参与排列。相离问题插空法:元素相离(即不相邻)问题,可先把无位置要求的几个元素全排列,再把规定的相离的几个元素插入上述几个元素的空位和两端。
解决排列组合问题,可采用以下技巧:首先,特殊元素优先考虑,如优先安排限制性大的元素。其次,面对排列组合混合问题,先选择后排列,简化复杂度。接着,处理相邻问题时,使用“捆绑”策略,将相邻元素视为整体;而相间问题则以“插空”法,找到元素插入的位置。定序问题则需通过除法进行处理,避免重复计算。
在做排列组合题时,我们需要根据题目要求确定是求排列还是组合。如果是排列,直接使用排列公式;如果是组合,先使用排列公式再除以m!。做题过程中,我们还需要注意以下几点: 确保理解题目要求,明确是求排列还是组合。 计算时,根据m和n的值,直接代入对应的公式计算。