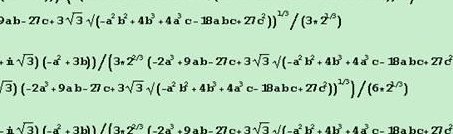三次方程（三次方程三个根之间的关系）

11-09 24阅读

三次方程的韦达定理

三次方程的韦达定理如下：aX^3+bX^2+cX+d=0。解法思想三次方程是未知项总次数最高为3的整式方程，其解法思想是通过配方和换元，使三次方程降次为二次方程。

三次方程韦达定理如下：一元三次方程的韦达定理是指一元三次方程axA3+bx^2+cx+d=0的三个解xxx3满足 X1+x2+x3=-b/a、X1x2+x1x3+x2x3=c/a、X1x2x3=-d/a其中a、b、c、d是常数。这个定理可以帮助我们快速求解一元三次方程。

（图片来源网络，侵删）

定理：对于一个三次方程，假设它的三个根分别为r、s、t，那么有以下关系：rs+st+tr=-c/a；rst=d/a；rst(rs+st+tr)=c^2/a^2-3d/a。

三次方韦达定理如下：三次方韦达定理是指对于一元三次方程ax^3+bx^2+cx+d=0，如果存在三个根xxx3，那么可以表示为x3=z*（x1^3）+（3ab-27d）x1/（2b^2-4a*c）以及对x2和x3进行类似的处理。其中，a、b、c、d是方程的系数，z是方程的一个解。

(x-x0)(x*x+dx+e)=0 其中d e由a b c唯一确定。后面就是解一元二次方程了。

三次方程求根公式

三次方程求根公式为：ax3+bx2+cx+d=0。标准型的一元三次方程aX^3+bX^2+cX+d=0（a，b，c，d∈R，且a≠0）其解法有：意大利学者卡尔丹于1545年发表的卡尔丹公式法；中国学者范盛金于1989年发表的盛金公式法。一元三次方程解法思想是：通过配方和换元，使三次方程降次为二次方程求解。

（图片来源网络，侵删）

三次方程求根公式如下：ax^3+bx^2+cx+d的标准型。化成x^3+(b/a)x^2+(c/a)x+(d/a)=0。可以写成x^3+a1*x^2+a2*x+a3=0。其中a1=b/a，a2=c/a，a3=d/a。令y=x-a1/3。则y^3+px+q=0。

三次方程求根公式：x^3+ax^2+bx+c=0。三次方程的求根公式如下：卡尔达诺公式（Cardanos formula）卡尔达诺公式给出了一般形式的三次方程的解法。对于形如ax+bx+cx+d=0的三次方程，卡尔达诺公式通过引入一个复数单位来计算出三个根的值。

三次方程形式为：ax3+bx2+cx+d=0。标准型的一元三次方程aX^3+bX^2+cX+d=0（a，b，c，d∈R，且a≠0）其解法有：意大利学者卡尔丹于1545年发表的卡尔丹公式法；中国学者范盛金于1989年发表的盛金公式法。

三次方程怎么求根?

1、三次方程求根公式为：ax3+bx2+cx+d=0。标准型的一元三次方程aX^3+bX^2+cX+d=0（a，b，c，d∈R，且a≠0）其解法有：意大利学者卡尔丹于1545年发表的卡尔丹公式法；中国学者范盛金于1989年发表的盛金公式法。一元三次方程解法思想是：通过配方和换元，使三次方程降次为二次方程求解。

2、三次方程求根公式如下：ax^3+bx^2+cx+d的标准型。化成x^3+(b/a)x^2+(c/a)x+(d/a)=0。可以写成x^3+a1*x^2+a2*x+a3=0。其中a1=b/a，a2=c/a，a3=d/a。令y=x-a1/3。则y^3+px+q=0。

3、三次函数求根公式为：aX^3+bX^2+cX+d=0（a，b，c，d∈R，且a≠0）。三次函数的求根公式就是一元三次方程的求根公式。因式分解法因式分解法不是对所有的三次方程都适用，只对一些三次方程适用。对于大多数的三次方程，只有先求出它的根，才能作因式分解。

4、三次方程求根公式：x^3+ax^2+bx+c=0。三次方程的求根公式如下：卡尔达诺公式（Cardanos formula）卡尔达诺公式给出了一般形式的三次方程的解法。对于形如ax+bx+cx+d=0的三次方程，卡尔达诺公式通过引入一个复数单位来计算出三个根的值。