正整数符号（正整数符号怎么打）

正整数的符号是什么?正整数集用什么表示?

正整数的符号是N或者N*。整数集用Z表示，实数集用R表示。在集合论里，自然数集N是包括元素“0”的。若是指一般的自然数(集)(即不包括元素“0”)用N+或N*表示，其中符号+或*是上标。

正整数集就是即所有正数且是整数的数的集合，是在自然数集中排除0的集合，一直到无穷大。正整数集通常用符号N+、N*、NN0表示。

正整数：和整数一样，正整数也是一个可数的无限集合。在数论中，正整数，即3……；但在集合论和计算机科学中，自然数则通常是指非负整数，即正整数与0的集合。整数：整数的全体构成整数集，整数集是一个数环。

实数、自然数、正整数、正数分别用什么字母表示?

实数R、自然数N、正整数N+、正数：+ 自然数，用以计量事物的件数或表示事物次序的数，即用数码0，1，2，3，4，……所表示的数，自然数由0开始 ， 一个接一个，组成一个无穷集体。整数是表示物体个数的数，0表示有0个物体，整数是人类能够掌握的最基本的数学工具，整数的全体构成整数集。

实数：R、自然数：N、正整数：N*(非零自然数)、整数：Z 实数：是有理数和无理数的总称。数学上，实数定义为与数轴上的实数，是有理数和无理数的总称。数学上，实数定义为与数轴上的实数，点相对应的数。实数可以直观地看作有限小数与无限小数，实数和数轴上的点一一对应。

有理数：Q 实数：R 整数 ：Z 正整数：Z+ 自然数：N。有理数 能表示为两个整数之比 如3，-911，7272…，7/22。无理数 不能表示为两个整数之比的数。 圆周率、2的平方根。性质不同：有理数：有理数为整数（正整数、0、负整数）和分数的统称。

实数、自然数和正数在数学中各自代表的字母是：自然数，通常用N来表示，它们是用于计数事物件数或表示事物顺序的数字，从0开始，连续不断。自然数集由0、3…组成。整数集，用Z表示，包括所有的整数，其中0代表没有物体，整数是数学中基本的计数工具。

实数用字母R表示。自然数用字母N表示，整数用字母Z表示。实数，是有理数和无理数的统称，分为正实数、0和负实数。有理数可以分成整数和分数，而整数可以分为正整数、零和负整数。无理数可以分为正无理数和负无理数。实数 定义：数学上，实数定义为与数轴上的点相对应的数。

正整数符号是什么呢?

正整数符号是“+”。正整数是大于零的整数，用于表示正数的基本符号就是加号。加号在许多文化和数学体系中都代表着增加、上升和前进的意义。正整数在计算机科学、数学、物理等多个领域都有广泛应用。在计算机编程中，加号常用来表示正整数的数值运算。

正整数用符号N+或N表示。正整数其中N是英文“正整数”的缩写。在数学中，正整数是指大于0的整数，通常包含4……等。这些数都具有非负数和自然数的属性，并且可以用符号+N或N来表示。正整数是数学中一个重要的概念，具有许多重要的性质和用途。

正整数符号为“+”或“+n”。在计算机编程中，通常用“+”表示正整数的数值。此外，“正整数”这一术语用来指代大于零的自然数集合中的任意一个整数。详细解释如下：正整数的定义 正整数是用于计量事物的数量的概念。即用大于零的整数表示数量的大小。

正整数的符号是N或者N*。整数集用Z表示，实数集用R表示。在集合论里，自然数集N是包括元素“0”的。若是指一般的自然数(集)(即不包括元素“0”)用N+或N*表示，其中符号+或*是上标。

正整数符号是N+。正整数也是一个可数的无限集合。在数论中，正整数，即3；但在集合论和计算机科学中，自然数则通常是指非负整数，即正整数与0的集合，也可以说成是除了0以外的自然数就是正整数。正整数又可分为质数，1和合数。正整数可带正号（＋），也可以不带。

数学中正整数的符号为n+,我想问“+”是在n的右上角还是水平..._百度...

正整数的符号为n+，其中的+是在n的后面，水平位置书写。详细解释如下：在数学中，正整数通常表示为n+，其中n代表一个具体的正整数，而+号表示该数是正数。这种表示方法主要是为了与负数进行区分，正数总是伴随着一个加号。

正整数集的符号是下标。详细解释如下：在正整数集的表达中，我们通常使用小写字母N作为符号，表示自然数集合，其中的数字为下标。这一符号的起源源于数学领域对集合的表达习惯。

结论：在数学的符号系统中，正整数的两种常见表示方法是N或N*。这个符号用于表示那些大于0的整数，它们是正数和整数的共同部分。正整数集合通常不包含0，如果需要排除0，会使用上标+或*来明确。整数集Z被用来代表所有的整数，无论是正、零还是负，它是数环结构的一部分。

正整数集的符号是“N＋”，详细介绍如下：正整数的定义和性质：正整数是大于零且没有小数部分的整数，可表示为4等。正整数性质是任意两个正整数的和仍然是正整数，正整数与0相乘得到0，正整数满足传递性等。

“n”字的大写是“N”。具体写法如下：左边的竖，从上到下 中间的斜，从左上到右下 右边的竖，从上到下 N， n 是拉丁字母英文字母中的第14个字母，n在代数中表示很多，如从1开始到2，到3，...， 到n。

正整数集的符号

正整数集就是即所有正数且是整数的数的集合，是在自然数集中排除0的集合，一直到无穷大。正整数集通常用符号N+、N*、NN0表示。

正整数集的符号为N+或N^*。正整数集是指用以计量正数的集合，即所有大于零的整数所构成的集合。它是自然数集中去掉0的部分，数学中常用符号来表示不同的数集。其中，N代表自然数集，包括所有非负整数。

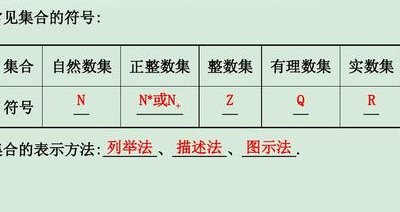
数学集合符号如下：N：非负整数集合或自然数集合{0，1，2，3，…}。N*或N+：正整数集合{1，2，3，…}。Z：整数集合{…，-1，0，1，…}。Q：有理数集合。Q+：正有理数集合。Q-：负有理数集合。R：实数集合(包括有理数和无理数）。R+：正实数集合。

数学集合符号有N、N+、Z、Q、R、C等。全体非负整数的集合通常简称非负整数集（或自然数集），记作N。非负整数集内排除0的集，也称正整数集，记作N+（或N*）。全体整数的集合通常称作整数集，记作Z。全体有理数的集合通常简称有理数集，记作Q。全体实数的集合通常简称实数集，记作R。

N＊（N＋）正自然数集。自然数：NN：自然数集，非负整数集（包含元素＂0＂）。N＊（N＋）正自然数集，正整数集（其中＊表示从集合中去掉元素“0”，如R＊表示非零实数）。P素数（质数）集。Q有理数集。R实数集。Z整数集。