空间向量相乘公式（空间向量相乘公式坐标公式）

非结构化数据如何可视化呈现？

1、信息可视化 信息可视化是一个跨学科领域，其核心在于利用视觉呈现手段来处理大规模的非数值型信息资源。这包括了软件系统中的文件、程序代码等复杂信息集合，以及抽象数据集如非结构化文本、高维空间中的点等。

2、数据可视化基础数据可视化是用图形方式呈现数据，帮助人们直观地捕捉隐藏信息。它并非简单地把数据变成图形，而是一种从数据视角探索世界的方式。 重要性揭示比如，数据可视化可助快速理解大量信息，比如通过对比和图形符号揭示联系。研究显示，人们记忆图像的速度远超文字，因此可视化数据能加深记忆和理解。

3、可视化呈现：揭示数据的秘密地图/借助图表和可视化工具，大数据分析就像一幅生动的画卷，清晰揭示数据的内在模式、趋势和关联。这种直观的方式不仅让复杂的数据变得易于理解，还能揭示隐藏在数据中的微妙洞察和规律。 数据挖掘算法：挖掘隐藏的知识金矿/大数据分析的科技支柱就是数据挖掘技术。

4、数据可视化展现 通过可视化展现形式，可直观呈现多维度数据表现，用于总结、汇报等。想要快速进行大数据分析，可通过新浪舆情通实现，系统一站式提供信息采集、大数据分析、可视化报告等服务，针对各行业还提供定制化大数据解决方案。

5、解说牌的信息可视化，是通过图形图像技术将非结构化文本等数据进行加工，提取有效信息，挖掘逻辑关联，以直观、有趣甚至可互动的方式进行系统性视觉传达。其目的是帮助观众理解展览中的海量信息，激发思考。解说牌设计应遵循人类大脑视觉认知规律，确保信息准确、科学、简洁且易于传达。

6、信息可视化是指通过利用图形图像方面的技术与方法，帮助人们理解和分析数据。信息可视化是一个跨学科领域，旨在研究大规模非数值型信息资源的视觉呈现（如软件系统之中众多的文件或者一行行的程序代码）。

空间向量相乘公式

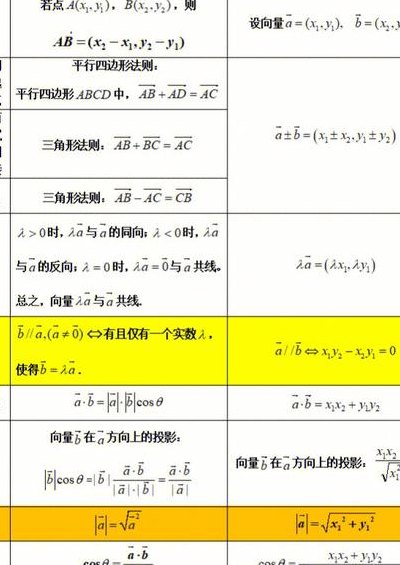
1、空间向量相乘公式最初以坐标形式表示，用两个三维空间向量来表示，形式为：点乘：A B = AxBx + AyBy + AzBz；叉乘：AB=(AyBz-AzBy， AzBx- AxBz， AxBy- AyBx)；相似乘积：A B：(AxxBx，AyyBy，AzzBz)。长度相等且方向相同的向量叫做相等向量．向量a与b相等，记作a=b。

2、空间向量乘积公式是：向量a=(x1，y1)，向量b=(x2，y2)，a·b=x1x2+y1y2=|a||b|cosθ(θ是a，b夹角)。空间中具有大小和方向的量叫做空间向量。向量的大小叫做向量的长度或模。规定，长度为0的向量叫做零向量，记为0。模为1的向量称为单位向量。

3、空间向量相乘有以下两种公式： 向量点积：向量 $\textbf{a}=(a_1，a_2，a_3)$ 和向量 $\textbf{b}=(b_1，b_2，b_3)$ 的点积为：$$\textbf{a}\cdot\textbf{b}=a_1b_1+a_2b_2+a_3b_3$$ 。

4、向量a=(x1，y1)，向量b=(x2，y2)；a·b=x1x2+y1y2=|a||b|cosθ(θ是a，b夹角)PS：向量之间不叫乘积，而叫数量积。如a·b叫做a与b的数量积或a点乘b 向量积，数学中又称外积、叉积，物理中称矢积、叉乘，是一种在向量空间中向量的二元运算。

5、向量相乘公式是：对于向量的数量积，计算公式为：A=(x1，y1，z1)，B=（x2，y2，z2），A与B的数量积为x1x2+y1y2+z1z2。其向量积，数学中又称外积、叉积，物理中称矢积、叉乘，是一种在向量空间中向量的二元运算。与点积不同，它的运算结果是一个向量而不是一个标量。

6、即叉乘。将向量用坐标表示（三维向量），若向量a=(a1，b1，c1)，向量b=(a2，b2，c2)，则 向量a·向量b=a1a2+b1b2+c1c2 向量a×向量b= | i j k| |a1 b1 c1| |a2 b2 c2| =(b1c2-b2c1，c1a2-a1c2，a1b2-a2b1)（i、j、k分别为空间中相互垂直的三条坐标轴的单位向量）。

向量相乘的公式是什么?

向量相乘公式如下：，（0°≤θ≤180°）向量积（向量相乘），数学中又称外积、叉积，物理中称矢积、叉乘，是一种在向量空间中向量的二元运算。与点积不同，它的运算结果是一个向量而不是一个标量。并且两个向量的叉积与这两个向量和垂直。其应用也十分广泛，通常应用于物理学光学和计算机图形学中。

向量积公式 向量积|c|=|a×b|=|a||b|sin 向量相乘分内积和外积 内积 ab=，a，b，cosα（内积无方向，叫点乘）外积 a×b=，a，b，sinα（外积有方向，叫×乘）那个读差，即差乘，方便表达所以用差。

向量a·向量b=|a||b|cos 在物理学中，已知力与位移求功，实际上就是求向量F与向量s的内积，即要用点乘。叉乘，也叫向量的外积、向量积。顾名思义，求下来的结果是一个向量，记这个向量为c。

两个坐标向量相乘是a*b=x1x2+y1y2=|a||b|cosθ。一般向量之间不叫乘积，而叫数量积，如a*b叫做a与b的数量积或a点乘b。平面向量是在二维平面内既有方向(direction)又有大小(magnitude)的量，物理学中也称作矢量，与之相对的是只有大小、没有方向的数量（标量）。

向量相乘公式是：对于向量的数量积，计算公式为：A=(x1，y1，z1)，B=（x2，y2，z2），A与B的数量积为x1x2+y1y2+z1z2。其向量积，数学中又称外积、叉积，物理中称矢积、叉乘，是一种在向量空间中向量的二元运算。与点积不同，它的运算结果是一个向量而不是一个标量。

空间向量相乘的公式有那两种?

空间向量相乘有以下两种公式： 向量点积：向量 $\textbf{a}=(a_1，a_2，a_3)$ 和向量 $\textbf{b}=(b_1，b_2，b_3)$ 的点积为：$$\textbf{a}\cdot\textbf{b}=a_1b_1+a_2b_2+a_3b_3$$ 。

空间向量相乘公式最初以坐标形式表示，用两个三维空间向量来表示，形式为：点乘：A B = AxBx + AyBy + AzBz；叉乘：AB=(AyBz-AzBy， AzBx- AxBz， AxBy- AyBx)；相似乘积：A B：(AxxBx，AyyBy，AzzBz)。长度相等且方向相同的向量叫做相等向量．向量a与b相等，记作a=b。

向量和向量间的运算有两种：点乘和叉乘。点乘“·”计算得到的结果是一个标量；a·b=|a||b|cosw(a、b上有向量标，不便打出。w为两向量角度)。叉乘“×”得到的结果是一个垂直于原向量构成平面的向量。