循环小数的概念（什么叫无限循环小数的概念）

循环小数是分数吗

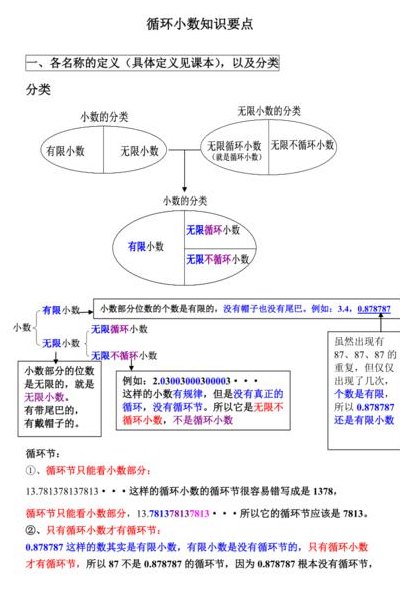
1、循环小数是分数。循环小数的定义是：一个数的小数部分从某一位起，一个或几个数字依次重复出现的无限小数，称为循环小数（circulating decimal）。循环小数之所以能化为分数，是因为它们具有周期性的结构。通过数学变换，可以将循环小数转化成分数形式。分数的概念源自对整体的分割。

2、循环小数是分数。从小数点后某一位开始依次不断地重复出现前一个或一节数字的十进制无限小数，叫做循环小数，如166..*（混循环小数），323232..（循环小数），333333…（循环小数）等，其中依次循环不断重复出现的数字叫循环节。

3、循环小数是分数，一个数的小数部分从某一位起，一个或几个数字依次重复出现的无限小数叫循环小数，循环小数会有循环节（循环点），并且可以化为分数。两个整数相除，如果得不到整数商，会有两种情况：一种，得到有限小数，另一种，得到无限小数。

循环小数一定是无限小数无限小数不一定是循环小数对吗

对的。循环小数指一个数的小数部分从某一位起一个或几个数字依次重复出现存，会无限循环下去，即小数位数无限，所以一定是无限小数。无限小数是指小数位数无限，但是这些数不一定存在循环，所以不一定是循环小数。循环节表示 循环节的表示方法。

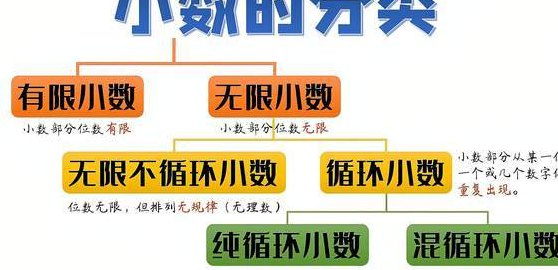
但是无限小数不一定是循环小数，无限小数中，包括无限循环小数和无限不循环小数两种，所以无限小数不一定是循环小数，无限小数中的无限不循环小数也就是无理数，比较熟悉的无限不循环小数有圆周率π、√√e等。愿我的回答对你有帮助！如有疑问请追问，愿意解疑答惑。

是的，循环小数一定是无限小数，但无限小数不一定是循环小数 纯小数：整数部分是0的小数叫做纯小数，纯小数比1小。如：0.190.140.15276都是纯小数。纯小数小于1，就是0.×××的形式。纯小数就是0到1之间的数，（大于0小于1），通俗的讲就是零点几（0.X）。

无限小数不一定是循环小数。循环小数可分为有限循环小数，如：123123123（不可添加省略号）和无限循环小数，如：123123123……（有省略号）。前者是有限小数，后者是无限小数。

无限小数指经计算化为小数后，小数部分无穷尽，不能整除的数。循环小数是指一个数的小数部分从某一位起，一个或几个数字依次重复出现的无限小数。无限小数范围大于循环小数。无限小数包含循环小数。循环小数是无限小数，但无限小数不一定是循环小数。

什么是循环小数

1、纯循环小数：自小数点后的十分位开始循环，比如：0.3333333……就是纯循环小数。混循环小数：自小数点后十分位不开始循环，后面才开始循环，比如：0.322222222222……就是混循环小数。

2、纯循环小数是一种具有特定模式的小数，其小数部分不含终止的位数，而是呈现出循环的无限延伸特性。简单来说，在一个小数中，如果出现某几个数字排列的重复性，这些数字会按照一定的次序持续不断地重复出现，这就是纯循环小数的表现形态。此类小数的特点是无限重复某一段数字序列，直至无穷尽。

3、一个数的小数部分从某一位起，一个或几个数字依次重复出现的无限小数叫循环小数（circulating decimal）。其中依次循环不断重复出现的数字叫循环节。循环小数会有循环节（循环点），并且可以化为分数。两个整数相除，如果得不到整数商，会有两种情况：一种，得到有限小数；另一种，得到无限小数。

4、循环小数是一个数的小数部分从某一位起，一个或几个数字依次重复出现的无限小数。循环小数分为纯循环小数和混循环小数两种。从小数部分第一位开始的循环小数，称为纯循环小数。纯循环小数是从十分位开始循环的小数，如0.3333333..(1/3)，0.14285714285.(1/7)等。