定积分的几何意义（定积分的几何意义求定积分）

利用定积分的几何意义

1、利用定积分的几何意义：是函数y=f(x)的曲线，与其定义域的区间[a，b]，即a≤x≤b所围成平面图形的面积。定积分是积分的一种，是函数f(x)在区间[a，b]上积分和的极限。

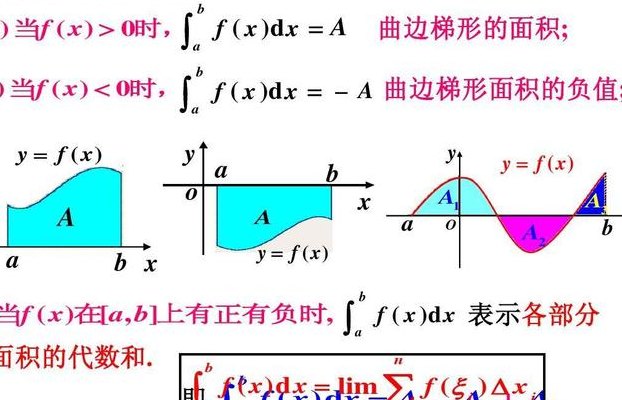
2、定积分的几何意义在于它代表被积函数与坐标轴围成的面积。具体地，x轴之上部分的面积被看作正值，x轴之下部分的面积则被看作负值。以余弦函数cosx在区间[0，2π]为例，其正负面积相抵，最终代数和为0。这揭示了定积分与几何图形之间的紧密联系。

3、定积分的几何意义是被积函数与坐标轴围成的面积，x轴之上部分为正，x轴之下部分为负，根据cosx在[0， 2π]区间的图像可知，正负面积相等，因此其代数和等于0。定积分是积分的一种，是函数f(x)在区间[a，b]上的积分和的极限。

4、面积，物体占据面积。面积：定积分可以用来计算曲线下面积。函数在区间a，b上非负，那么定积分表示的就是由曲线y等于fx与直线x等于a，x等于b及x轴围成的曲边梯形的面积。

5、定积分的几何意义是被积函数与坐标轴围成的面积。定积分属于积分的一种，它反映了函数f（x）在区间（a，b）内积分和的极限。其几何意义在于求解由y=0、x=a、x=b以及y=f（x）所围成的图形的面积，该图形被称为曲边梯形，而在某些特定情况下，它可能退化为曲边三角形。

6、详细解释 定积分的几何意义可以从两个方面来理解。首先，从直观上来说，定积分可以理解为曲线与坐标轴围成的面积。这个面积可以通过对函数进行积分来求解。其次，从数学的角度来看，定积分是一种特殊的极限形式，它可以用来求解一些复杂函数的累加和或近似值。

定积分等于零的几何意义

1、定积分的几何意义是被积函数与坐标轴围成的面积，其中x轴之上部分为正面积，x轴之下部分为负面积。例如，cosx在[0，2π]区间内的图像表明，正面积与负面积相等，因此整个区域的代数和等于零。定积分是一种积分形式，具体来说是函数f(x)在区间[a，b]上积分和的极限。

2、∫sinxdx=0证明如下：定积分就是求函数f(X)在区间[a，b]中的图像包围的面积，即由 y=0，x=a，x=b，y=f(X)所围成图形的面积。这个图形称为曲边梯形，特例是曲边三角形。一个函数，可以存在不定积分，而不存在定积分；也可以存在定积分，而不存在不定积分。

3、积分的几何意义是被积函数与坐标轴围成的面积，x轴之上部分为正，x轴之下部分为负，根据cosx在[0， 2π]区间的图像可知，正负面积相等，因此其代数和等于0。

定积分的几何意义是什么

1、定积分的几何意义是被积函数与坐标轴围成的面积，x轴之上部分为正，x轴之下部分为负，根据cosx在[0， 2π]区间的图像可知，正负面积相等，因此其代数和等于0。定积分是积分的一种，是函数f(x)在区间[a，b]上的积分和的极限。

2、定积分的几何意义在于它代表被积函数与坐标轴围成的面积。具体地，x轴之上部分的面积被看作正值，x轴之下部分的面积则被看作负值。以余弦函数cosx在区间[0，2π]为例，其正负面积相抵，最终代数和为0。这揭示了定积分与几何图形之间的紧密联系。

3、定积分在几何上，具有明确的实际意义。它主要表示曲线与坐标轴所夹的面积，也可以表示某些立体图形的体积。具体来说： 表示曲线与坐标轴之间的面积 当函数y=f在区间[a，b]上连续时，我们可以通过定积分来求解该函数图像与x轴所夹的平面面积。

4、定积分的几何意义是被积函数与坐标轴围成的面积。定积分属于积分的一种，它反映了函数f（x）在区间（a，b）内积分和的极限。其几何意义在于求解由y=0、x=a、x=b以及y=f（x）所围成的图形的面积，该图形被称为曲边梯形，而在某些特定情况下，它可能退化为曲边三角形。

定积分的几何意义

1、定积分的几何意义是被积函数与坐标轴围成的面积，x轴之上部分为正，x轴之下部分为负，根据cosx在[0， 2π]区间的图像可知，正负面积相等，因此其代数和等于0。定积分是积分的一种，是函数f(x)在区间[a，b]上的积分和的极限。

2、定积分的几何意义是被积函数与坐标轴围成的面积，其中x轴之上部分为正面积，x轴之下部分为负面积。例如，cosx在[0，2π]区间内的图像表明，正面积与负面积相等，因此整个区域的代数和等于零。定积分是一种积分形式，具体来说是函数f(x)在区间[a，b]上积分和的极限。

3、定积分的几何意义在于它代表被积函数与坐标轴围成的面积。具体地，x轴之上部分的面积被看作正值，x轴之下部分的面积则被看作负值。以余弦函数cosx在区间[0，2π]为例，其正负面积相抵，最终代数和为0。这揭示了定积分与几何图形之间的紧密联系。

4、定积分的几何意义是：1，当f(x)为正时，此函数在某一区间的定积分表示x轴上方函数所围成的面积。2，当f(x)为在某一给定区间为负时，定积分表示函数在x轴下方所围面积的相反数，即负数。3，当f(x)在某一区间有正有负时，定积分表示函数在x轴上方围成的面积减去x轴下方围成的面积的值。

定积分的几何意义?

定积分的几何意义是被积函数与坐标轴围成的面积，x轴之上部分为正，x轴之下部分为负，根据cosx在[0， 2π]区间的图像可知，正负面积相等，因此其代数和等于0。定积分是积分的一种，是函数f(x)在区间[a，b]上的积分和的极限。

定积分的几何意义在于它代表被积函数与坐标轴围成的面积。具体地，x轴之上部分的面积被看作正值，x轴之下部分的面积则被看作负值。以余弦函数cosx在区间[0，2π]为例，其正负面积相抵，最终代数和为0。这揭示了定积分与几何图形之间的紧密联系。

定积分的几何意义 定积分在几何上，具有明确的实际意义。它主要表示曲线与坐标轴所夹的面积，也可以表示某些立体图形的体积。具体来说： 表示曲线与坐标轴之间的面积 当函数y=f在区间[a，b]上连续时，我们可以通过定积分来求解该函数图像与x轴所夹的平面面积。

定积分具有几何意义吗?

是的。定积分的几何意义是：1，当f(x)为正时，此函数在某一区间的定积分表示x轴上方函数所围成的面积。2，当f(x)为在某一给定区间为负时，定积分表示函数在x轴下方所围面积的相反数，即负数。

定积分在几何上，具有明确的实际意义。它主要表示曲线与坐标轴所夹的面积，也可以表示某些立体图形的体积。具体来说： 表示曲线与坐标轴之间的面积 当函数y=f在区间[a，b]上连续时，我们可以通过定积分来求解该函数图像与x轴所夹的平面面积。

除了几何意义外，定积分还在物理、工程等多个领域有着广泛的应用，例如在求解物体的质心、计算曲线长度、求解变力做功等方面都有定积分的身影。

定积分的几何意义在于它代表被积函数与坐标轴围成的面积。具体地，x轴之上部分的面积被看作正值，x轴之下部分的面积则被看作负值。以余弦函数cosx在区间[0，2π]为例，其正负面积相抵，最终代数和为0。这揭示了定积分与几何图形之间的紧密联系。

定积分的几何意义是被积函数与坐标轴围成的面积，x轴之上部分为正，x轴之下部分为负，根据cosx在[0， 2π]区间的图像可知，正负面积相等，因此其代数和等于0。定积分是积分的一种，是函数f(x)在区间[a，b]上的积分和的极限。

定积分的几何意义是被积函数与坐标轴围成的面积。定积分的运用 在几何方面，定积分可以用来计算平面图形的面积、旋转体的体积、曲线的弧长以及旋转体的侧面积等。