割线定理（什么是切割线定理）

割线定理如何推导?

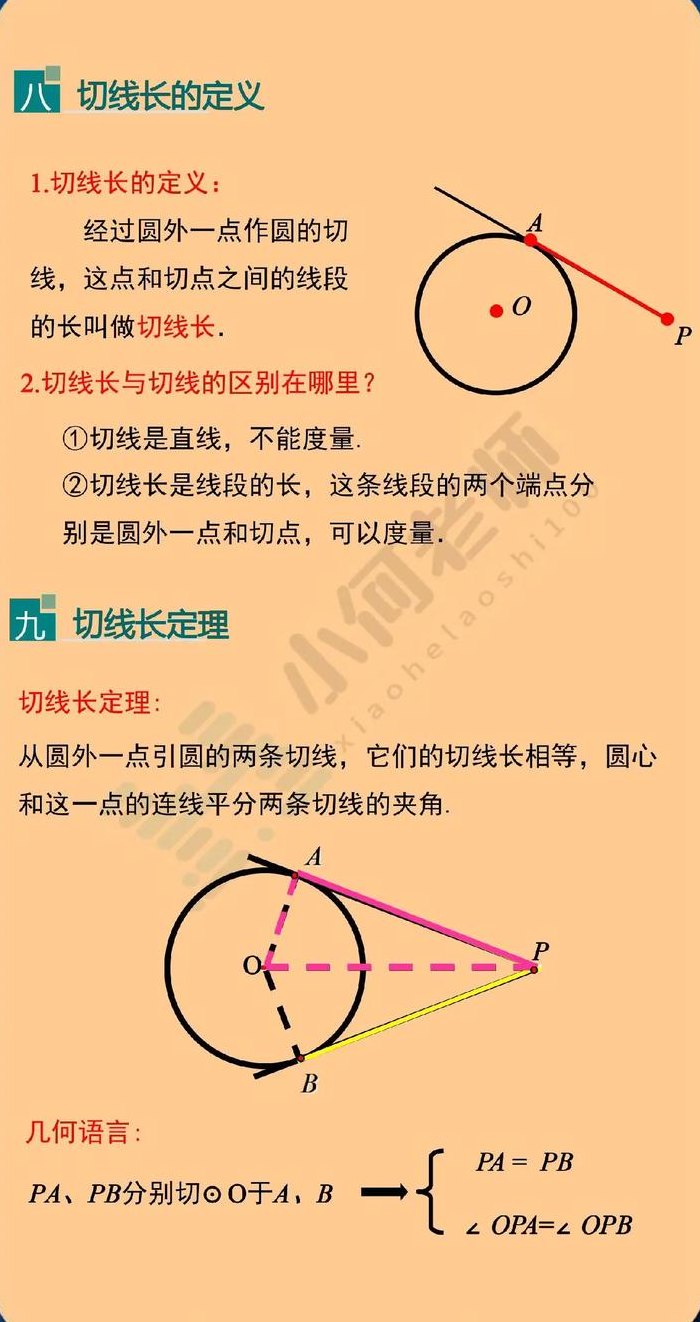
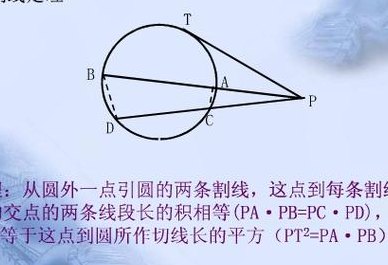
切割线定理的证明方法如下：从圆外的一点引入圆的切线和割线。切线长度是从该点到正割线和圆的交点的两条线段长度之比的中间项。割线定理的推论：从圆外的一点引入一个圆的两条割线，从该点到每一条割线与圆的交点的两条线段的长度之积相等。割线定理是指从圆外一点引出一个圆的两条割线。

切割线定理推论：从圆外一点引圆的两条割线，这一点到每条割线与圆的交点的两条线段长的积相等。几何语言表达为：TC=PBA，PDC是⊙O的割线，则PD·PC=PA·PB。综上可知：PT^2=PA·PB=PC·PD。切割线定理证明：设ABP是⊙O的一条割线，PT是⊙O的一条切线，切点为T，则PT^2=PA·PB。

割线定理是指在平面上有一条割线，它与两条相交弦相交于两点，这条割线与两条相交弦构成的和满足特定的数学关系。具体地，从每个交点向割线做垂线，这两条垂线的长度乘积等于割线与两条弦交点的连线段的乘积。简单地说，割线定理描述了平面上割线与两相交弦之间的几何关系。

证明过程如下：首先，连接CE和DB。由于∠E和∠B都共同夹着弧CD，根据圆周角定理，∠E等于∠B。同时，注意到∠EPC和∠BPD也是相等的。这就意味着三角形PCE和PDB相似，根据相似三角形的比例关系，我们得到PC与PD的比等于PE与PB的比，从而得出PC·PB=PD·PE的结论。

这个结论可以通过圆周角定理和相似三角形的性质推导出来，进而证明了割线定理。进一步的，如果延长割线至切线，如PT是⊙O的切线，那么PT的平方等于点P到割线的交点A和B的距离的乘积，即PT^2=PA·PB。

割线定理

1、割线定理：通过圆外一点的两条割线（或称切线）所构成的两个夹角之和等于所对应的相交弦所对应的圆心角。即两条从同一点出发，相交于圆上的割线与圆心连线所夹的两个角之和等于这两条割线所夹的弦所对应的圆心角。

2、割线定理是指在平面上有一条割线，它与两条相交弦相交于两点，这条割线与两条相交弦构成的和满足特定的数学关系。具体地，从每个交点向割线做垂线，这两条垂线的长度乘积等于割线与两条弦交点的连线段的乘积。简单地说，割线定理描述了平面上割线与两相交弦之间的几何关系。

3、割线定理：从圆外一点引割线交圆于两点，这一点与割线两端点的距离之积等于该点与圆心的距离的平方与该点所在弦的平方的差。详细解释如下：割线定理的定义 当从圆外的一个特定点引出一条割线，这条割线与圆的两个交点之间的线段被称为割线段。

4、割线定理，也被称为切割线定理，是一个几何学中的重要定理，它描述了从圆外一点P引出的两条割线与圆相交于A、B两点时，PA与PB的乘积等于PC与PD的乘积，即PA·PB = PC·PD。当PA等于PB，即直线AB与圆相切时，这个关系简化为PA = PC·PD，这是切线定理的一个特例。

割线的割线定理

割线定理：从圆外一点引割线交圆于两点，这一点与割线两端点的距离之积等于该点与圆心的距离的平方与该点所在弦的平方的差。详细解释如下：割线定理的定义 当从圆外的一个特定点引出一条割线，这条割线与圆的两个交点之间的线段被称为割线段。

割线的割线定理：割线定理是在圆内的一个线段，其两个端点都在圆上，如果从这条线段向外引出一条割线，那么这条割线被线段所截得的两条线段的比例等于这两段线段与相对应的两段圆弧的比例。详细解释如下：首先，明确割线的割线定理的定义。在一个给定的圆中，有一条线段AB连接圆上的两点A和B。

割线割线定理，也被称为Secant Theorem，是关于圆的一个几何性质。当从圆外一点P引两条割线，与圆相交于C、B、D、E各点时，一个关键的性质是点P到每条割线与圆的交点距离的乘积相等。具体来说，如图所示，如果PA是切线，那么有PC·PB=PD·PE。

这个结论可以通过圆周角定理和相似三角形的性质推导出来，进而证明了割线定理。进一步的，如果延长割线至切线，如PT是⊙O的切线，那么PT的平方等于点P到割线的交点A和B的距离的乘积，即PT^2=PA·PB。

割线定理，也被称为切割线定理，是一个几何学中的重要定理，它描述了从圆外一点P引出的两条割线与圆相交于A、B两点时，PA与PB的乘积等于PC与PD的乘积，即PA·PB = PC·PD。当PA等于PB，即直线AB与圆相切时，这个关系简化为PA = PC·PD，这是切线定理的一个特例。

什么是圆的三大切线定理?

圆的三大切线定理是指与同一个圆相切的三条切线之间的关系。这三大切线定理分别是：内切角定理、割线定理和切分线定理。内切角定理：任意一条切线与半径所构成的夹角等于其对顶的弧所对应的圆心角。换句话说，切线与半径的夹角等于所对应的切点处的弧的角度。

圆的三大切线定理是关于圆与其内接三角形的切线性质的定理。它们包括以下三个定理： 切线定理（外切线定理）：如果从一个点与圆外切，则这个切点与圆心以及这个点构成的直线是垂直的。 切角定理（切割角定理）：如果从一个点引两条切线与圆相切，则这两条切线所夹的角是相等的。

当涉及到圆的三个切线定理时，以下是相应的公式： 切线定理一（切线与半径垂直定理）：如果切点坐标为 (x， y)，圆心坐标为 (a， b)，则从切点到圆心的向量为 (a - x， b - y)。

第一个定理，就是切线的性质定理，这个定理是很简单的，而且理解不困难，只要记住：”过圆心“，”过切点“和”互相垂直“这三条谁知二推一就够了。第二个定理，是切线的判定定理，切线的判定是中考中常经常考的内容，切线判定主要有三种方式：定义法、距离法及定理法。