球面距离（球面距离最短证明）

球面距离怎么求

1、球面距离计算公式：d(x1，y1，x2，y2)=r*arccos(sin(x1)*sin(x2)+cos(x1)*cos(x2)*cos(y1-y2))x1，y1是纬度\经度的弧度单位，r为地球半径 而当y1=y2时，公式就变为：d=r*|x1-x2| 球面上有三个点A、B、C。

2、先将两个点分别与球心连线，得到一个夹角，算出这个夹角的大小，然后根据球的半径算出周长，用周长乘以夹角，再除360就是球面距离。

3、球面距离公式是S=R·arcos[cosβcos（α1-α2）+sinβ]，球面上两点之间的最短连线的长度，就是经过这两点的大圆在这两点间的一段劣弧的长度。地球形状是一个两极部位略扁的不规则的球体。地球的平均半径为6371千米，赤道半径6378千米，极半径6357千米。赤道周长约为4万千米。零度经线叫做本初子午线。

球面距离怎么算?

球面距离计算公式：d(x1，y1，x2，y2)=r*arccos(sin(x1)*sin(x2)+cos(x1)*cos(x2)*cos(y1-y2))，其中，x1，y1是纬度经度的弧度单位，r为地球半径。而当y1=y2时，公式就变为：d=r*|x1-x2|球面上有三个点A、B、C。

先将两个点分别与球心连线，得到一个夹角，算出这个夹角的大小，然后根据球的半径算出周长，用周长乘以夹角，再除360就是球面距离。

球面距离公式是S=R·arcos[cosβcos（α1-α2）+sinβ]，球面上两点之间的最短连线的长度，就是经过这两点的大圆在这两点间的一段劣弧的长度。地球形状是一个两极部位略扁的不规则的球体。地球的平均半径为6371千米，赤道半径6378千米，极半径6357千米。赤道周长约为4万千米。零度经线叫做本初子午线。

球面距离公式地球上两点球面距离公式

β1=β2=β，球面距离公式为：R·arcos[cosβcosβcos（α1-α2）+sinβsinβ] （II）α1=α2=α，球面距离公式为：R·arcos（cosβ1cosβ2+sinβ1sinβ2）=R·arcoscos（β1-β2） （III）实例1：在北纬45°纬线上，A、B两点球面距离为R，A位于东经20°，求B点的位置。

cosb*cosy*(cosa*cosx+sina*sinx)+sinb*siny=cosb*cosy*cos(a-x)+sinb*siny 因此AB两点的球面距离为 R*{arccos[cosb*cosy*cos(a-x)+sinb*siny]} 注：x，y，a，b都是角度，最后结果中给出的arccos因为弧度形式。所谓的“东经为正，西经为负，北纬为正，南纬为负”是为了计算的方便。

球面距离公式是计算球面上两点间距离的公式。设所求点A ，纬度角β1 ，经度角α1 ；点B ，纬度角β2 ，经度角α2。则距离 S=R·arc cos[cosβ1cosβ2cos（α1-α2）+sinβ1sinβ2]，其中R为球体半径。

球面距离公式是S=R·arcos[cosβcos（α1-α2）+sinβ]，球面上两点之间的最短连线的长度，就是经过这两点的大圆在这两点间的一段劣弧的长度。地球形状是一个两极部位略扁的不规则的球体。地球的平均半径为6371千米，赤道半径6378千米，极半径6357千米。赤道周长约为4万千米。

地球两点间距离计算公式如下 计算地球上两点间的距离可以使用球面三角学来估算。最常用的方法是使用haversine公式，这是一种根据经纬度计算大圆航线距离的方法。

如果我们假设地球半径为R。设第一点A的经纬度为(LonA， LatA)，第二点B的经纬度为(LonB， LatB)，东经取经度的正值(Longitude)，西经取经度负值(-Longitude)，北纬取90-纬，南纬取90+纬度值(90+Latitude)，则经过上述处理过后的两点被计为(MLonA， MLatA)和(MLonB， MLatB)。

球面距离的算法,地理上用的谁会给我详细的教一下。要详细啊。

1、不同经纬度上两点之间的球面距离：先计算两地的南北距离（纬度差*111千米），再计算两地的东西距离（经度差*111千米），再用勾股定理计算斜边长度，即为两地的球面距离。

2、如一点是东经120度，北纬10度。另一点是东经150度，北纬30度，那么这两点之间的距离就是：[（150-120）*111]的平方+[（30-10）*111]的平方，然后把得出的数据再开方，就是两点之间的距离。当然这种计算方法只是估算法，而且适用于低纬度地区。

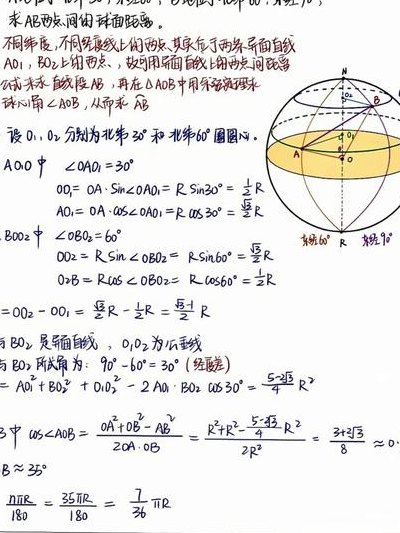
3、β2∈[-π/2，π/2 ]，AB =Rarccos[cosβ1cosβ2cos（α1-α2）+sinβ1sinβ2]利用勾股定理与正弦定理则可求出AB两点间的直线距离，在利用正弦定理可求出AB两点与地球0点夹角的度数，再利用如下公式：角EOD的度数/360度=E与D之间的球面距离/大圆周长，则可求出AB的球面距离。

4、你好！准确的说是近轴条件下可以简单的认为球面镜的焦距等于镜面曲率半径的一半。可以画一个半球凹面镜，（圆心为O点）模拟一条近轴光线入射，法线为入射点与原点的连线（半径），出射光线与光轴交于M点（1/2半径）处，从入射点到光轴作垂线，交光轴于P点。