子集的个数（子集的个数公式）

昨天 9阅读

子集的个数公式是

子集个数的公式是2的n次方，其中n为原集合的元素个数。这个公式可以被证明为正确的，在计算机科学和数学中被广泛应用。

子集个数公式：若一个集合中有n个元素，则这个集合的子集的个数为2^n个，真子集的个数为2^n-1个。其中，2表示可以从A中取出一个元素或不取出元素，n表示A中有n个元素，也就是说A中有n种取法，每种取法都可以构成一个子集，因此A的子集的个数为2^n。

（图片来源网络，侵删）

子集个数公式：若一个集合中有n个元素，则这个集合的子集的个数为2^n个，真子集的个数为2^n-1个。子集是一个数学概念：如果集合A的任意一个元素都是集合B的元素，那么集合A称为集合B的子集。符号语言：若_a∈A，均有a∈B，则A_B。

集合的子集个数公式为：子集个数=2^n，真子集个数2^n-1，非空子集个数2^n-1，非空真子集2^n-2。任何一个集合是它本身的子集，因此子集个数=2^n，真子集个数即减去本身，非空子集减去空集。如果集合A的任意一个元素都是集合B的元素，那么集合A称为集合B的子集。

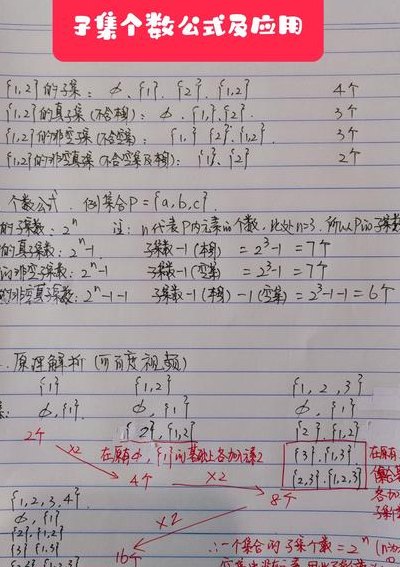
子集个数公式如下：子集、真子集个数计算公式对于含有n个元素的有限集合M，其子集、真子集、非空子集、非空真子集的个数依次为2n，2n－1，2n－1，2n－2。一个集合A={xl1，2}的子集有空集｛1}、｛2}、｛1，2}共4个子集，也就是一个集合的子集是包括这个集合本身的。

子集的个数怎么算的

子集个数的公式是2的n次方，其中n为原集合的元素个数。这个公式可以被证明为正确的，在计算机科学和数学中被广泛应用。

（图片来源网络，侵删）

子集的个数可以通过幂集PowerSet的方式来计算，其个数等于2的n次方，其中n为集合元素的个数。幂集的定义幂集是指一个集合的所有子集构成的集合。例如，对于集合{1，2，3}，其幂集为{{}，{1}，{2}，{3}，{1， 2}，{1，3}，{2，3}，{1，2，3}}。

的子集个数计算过程：已知一个里有n个元素（的C代表组合，其中nCr代表从n个元素内选取r个元素进行组合）：首先子集中元素有0个的有[nC0]。子集元素有1个的有[nC1]。子集元素有2个的有[nC2]。子集元素有m个的有[nCm]。子集元素有n-1个的有[nC（n-1）]。子集元素有n个的有[nCn]。