垂直渐近线（垂直渐近线和铅直渐近线一样吗）

三种渐近线公式是什么?

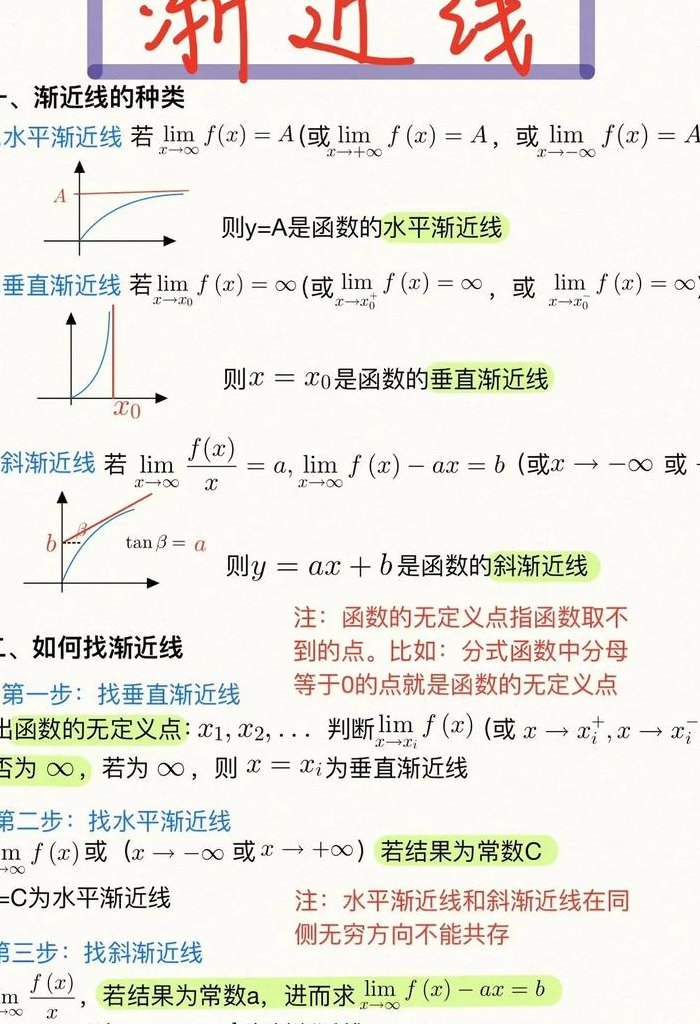
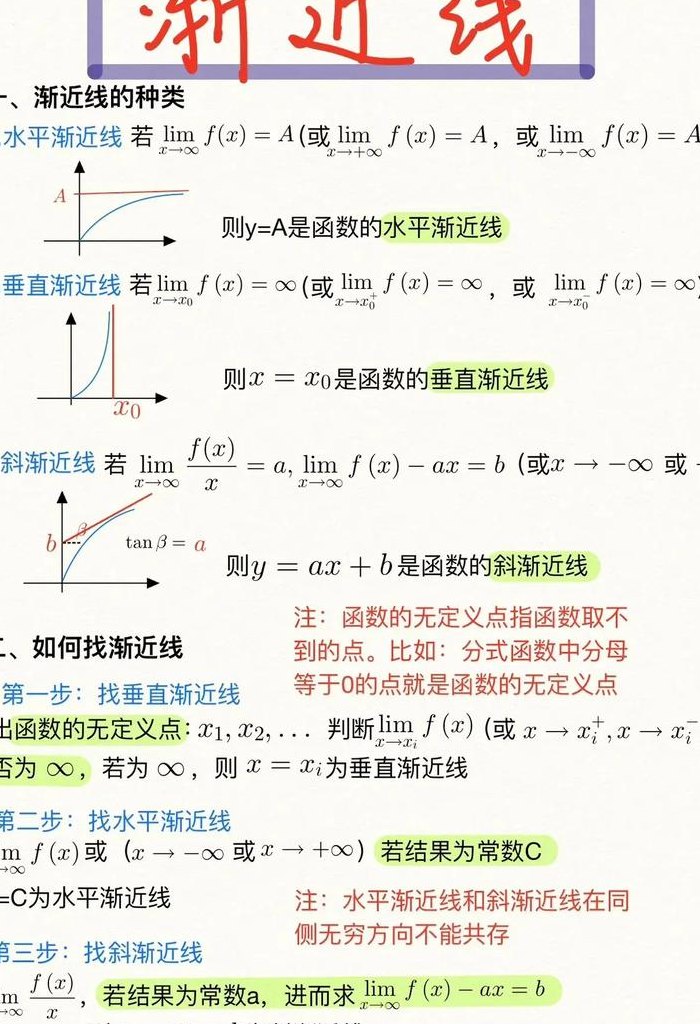
三种渐近线公式： 垂直渐近线公式：x = a。垂直渐近线出现在函数图形趋于无穷大或无穷小的垂直方向上的直线。例如，对于函数y = 1/x，其垂直渐近线为y轴，即x=0处。 水平渐近线公式：y = b 或 y = kx + b。水平渐近线出现在函数图形水平方向趋于无穷大或无穷小的直线。

三个求渐近线的公式：二次函数渐近线公式、反比例函数渐近线公式、幂函数渐近线公式。二次函数渐近线公式 对于形如 y = ax^2 + bx + c 的二次函数，其渐近线方程可以通过公式求得：y = ±√(4ac - b^2) / 2a。这个公式是二次函数的重要性质之一，用于确定函数的极限行为。

三种渐近线公式是：水平渐近线：x→＋∞或－∞时，y→c，y=c就是f（x）的水平渐近线；比如y=0是y=e^x的水平渐近线。铅直渐近线：x→a时，y→＋∞或－∞，x=a就是f（x）的铅直平渐近线；比如x=0是y=1/x的铅直渐近线。

渐近线的公式如下：1，水平渐近线：x→+∞或-∞时，y→c，y=c就是f(x)的水平渐近线；比如y=0是y=e^x的水平渐近线。2，铅直渐近线：x→a时，y→+∞或-∞，x=a就是f(x)的铅直平渐近线；比如x=0是y=1/x的铅直渐近线。

y=a^x+b/x+c，其中a，b，c为常数。渐近线有三种类型：垂直渐近线、水平渐近线、斜渐近线。垂直渐近线是指函数图像在无穷远处与x轴的交点，即x趋于无穷大时y趋于一个常数。水平渐近线是指函数图像在无穷远处与y轴的交点，即y趋于一个常数时x趋于无穷大。

水平渐近线：就是指在函数f(x)中，x→+∞或-∞时，y→c，y=c就是f(x)的水平渐近线。所以我们需要考虑的是x无限变大或者变小后，y的变化情况。斜渐近线：这种渐近线的形式为y=kx+b，反映函数在无穷远点的性态，先求k，k=limf(x)/x，再求b，b=limf(x)-kx。

什么是垂直渐近线和斜渐近线?

1、垂直渐近线：就是指当x→C时，y→∞。一般来说，满足分母为0的x的值C，就是所求的渐进线。x = C 就是垂直渐进线。水平渐近线：就是指在函数f(x)中，x→+∞或-∞时，y→c，y=c就是f(x)的水平渐近线。所以我们需要考虑的是x无限变大或者变小后，y的变化情况。

2、垂直：x趋向于b时，y趋向于无穷，则x=b是垂直渐近线。斜：当x趋向于无穷时，函数y=f(x)无限接近一条固定直线y=Ax+B，即斜渐近线。具体求法：x趋向于无穷时，limy/x=A，lim[y-Ax]=B，则有y=Ax+B是斜渐近线。

3、垂直渐近线：找到函数间断点，设其为b，求x→b时的函数极限，如果极限为∞，则x=b是函数的垂直渐近线。斜渐近线：斜率k=y/x在x→∞的极限。

4、垂直渐近线：如果函数在某一点的导数趋近于无穷大或无穷小，那么曲线可能在该点有垂直渐近线。找出函数的导数并解出无穷大的解即可确定垂直渐近线。 斜渐近线（斜线渐近线）：对于某些函数，可能会存在斜渐近线，即曲线在无穷远处逐渐接近某一直线。

5、要求渐近线，就是求极限，水平、垂直和斜的，思考要全面。三种渐近线：若limf(x)=C，x趋于无穷，则有水平渐近线y=C；若limf(x)=无穷，x趋于x。，则有垂直渐近线x=x。；若limf(x)/x=k不等于0，x趋于无穷，lim(f(x)-kx)=b， x趋于无穷，则有些渐近线y=kx+b。

6、一种是垂直渐近线：这种渐近线的形式为x=a，也就是函数在x=a处的值为无穷大。所以求这种渐近线的时候只要找函数的特殊点，然后验证在该点的函数值是否为无穷大即可。另一种是斜渐近线：这种渐近线的形式为y=kx+b，反映函数在无穷远点的性态。先求k，k=limf(x)/x，再求b，b=limf(x)-kx。

垂直渐近线找哪些点

1、y=e^x/(x+2)(x-1) 求垂直渐近线 (1) 先找出间断点，为x=-2和x=1 (2) 计算lim x→-2 y =lim x→-2 e^x/(x+2)(x-1) =∞ 同理，计算lim x→1 e^x/(x+2)(x-1)=∞ (3) 所以x=-2和x=1是y的垂直渐近线。

2、求垂直渐近线 (1)先找出间断点，为x=-2和x=1 (2)计算lim x→-2 y =lim x→-2 e^x/(x+2)(x-1)=∞ 同理，计算lim x→1 e^x/(x+2)(x-1)=∞ (3)所以x=-2和x=1是y的垂直渐近线。

3、该情况所需具体条件如下：要找到函数的定义域，定义域是函数能够取值的范围。接下来需要寻找函数在定义域上的极限，函数在某个点的左极限和右极限都不存在或者有限的，这个点就是垂直渐近线的潜在位置。对于一个函数 ，其在某个点a处的极限不存在或者有限的，垂直渐近线的方程可以写为x等于a。

4、具体来说，当函数在某一点左侧的导数趋向于正无穷或负无穷，右侧的导数也趋向于正无穷或负无穷时，该点就是垂直渐近线的潜在位置。通过这种方法，可以系统地找到函数的所有垂直渐近线。值得注意的是，判断垂直渐近线和水平渐近线的过程不仅有助于理解函数的极限行为，还能揭示函数在特定点附近的特殊性质。

5、垂直渐近线（垂直于x轴）和水平渐近线（平行于x轴）：需要给y求极限（x趋近于正无穷和负无穷各求一次），有极限那么就有水平渐近线。再看函数的定义域，如果没有间断点，那么肯定没有垂直渐近线，如果有间断点，那么需要判断在这些间断点的左导数和右导数是否为无穷大，如果是，那么就有垂直渐近线。

6、垂直渐近线是指曲线在某一点附近无限接近于某条垂直于x轴的直线，但不会与该直线相交。要确定一个函数是否具有垂直渐近线，首先需要检查函数的定义域中是否存在间断点。如果存在间断点，那么这些点可能成为垂直渐近线的候选位置。

什么是垂直渐近线,水平渐近线?

1、垂直渐近线：垂直渐近线则是指函数的图形表现为无限趋近于垂直于x轴的某一条直线。这种情况通常发生在某些分式函数中，当分母趋近于零而分子非零时，函数值趋于无穷大，对应的垂直线即为垂直渐近线。具体来说，如果函数f在x趋于某常数c时趋于无穷大或无穷小，那么x=c的垂直线就是该函数的垂直渐近线。

2、水平渐近线和垂直渐近线是与图形的渐近行为有关的概念，通常用于描述函数或曲线的特定性质。这两种渐近线与函数图像在极限情况下的趋势有关。水平渐近线（Horizontal Asymptote）：一条水平渐近线是指函数图像在无穷远处趋近于某个水平线的现象。

3、垂直渐近线：就是指当x→C时，y→∞。一般来说，满足分母为0的x的值C，就是所求的渐进线。x = C 就是垂直渐进线。水平渐近线：就是指在函数f(x)中，x→+∞或-∞时，y→c，y=c就是f(x)的水平渐近线。所以我们需要考虑的是x无限变大或者变小后，y的变化情况。

4、垂直渐近线：一般的垂直线是 x=k，如果当 x 趋近于某数 b 时，y 会趋近于无限大或负无限大时，那 x=b 就是垂直渐近线，一般来说大部份是让分母为 0 时。并不是所有曲线都有渐近线，渐近线反映了某些曲线在无限延伸时的变化情况。

5、水平渐近线：水平渐近线是一条平行于x轴的直线。当函数的自变量趋于无穷大或无穷小时，函数的值趋近于某一定值，即函数图像平行于这条直线并趋近于它。这种渐近线的方程形式通常为y=k。也就是说，不论自变量如何变化，函数值始终围绕某一固定值变化。

6、水平渐近：一般水平线的方程式是 y=k，水平渐近线是指当 x 趋近于无限大或负无限大时，y 会不会有极限值，如果 y 有极限值 a ，则 y=a 就是水平渐近线。

水平渐近线和垂直渐近线的定义是什么?

垂直渐近线：垂直渐近线则是指函数的图形表现为无限趋近于垂直于x轴的某一条直线。这种情况通常发生在某些分式函数中，当分母趋近于零而分子非零时，函数值趋于无穷大，对应的垂直线即为垂直渐近线。具体来说，如果函数f在x趋于某常数c时趋于无穷大或无穷小，那么x=c的垂直线就是该函数的垂直渐近线。

水平渐近：一般水平线的方程式是 y=k，水平渐近线是指当 x 趋近于无限大或负无限大时，y 会不会有极限值，如果 y 有极限值 a ，则 y=a 就是水平渐近线。

水平渐近线和垂直渐近线是与图形的渐近行为有关的概念，通常用于描述函数或曲线的特定性质。这两种渐近线与函数图像在极限情况下的趋势有关。水平渐近线（Horizontal Asymptote）：一条水平渐近线是指函数图像在无穷远处趋近于某个水平线的现象。

垂直渐近线：就是指当x→C时，y→∞。一般来说，满足分母为0的x的值C，就是所求的渐进线。x = C 就是垂直渐进线。水平渐近线：就是指在函数f(x)中，x→+∞或-∞时，y→c，y=c就是f(x)的水平渐近线。所以我们需要考虑的是x无限变大或者变小后，y的变化情况。

垂直渐近线怎么求

垂直渐近线求法如下：若limf(x)=C，x趋于无穷，则有水平渐近线y=C；若limf(x)=无穷，x趋于x。，则有垂直渐近线x=x。；若limf(x)/x=k不等于0，x趋于无穷，lim(f(x)-kx)=b，x趋于无穷，则有些渐近线y=kx+b。水平的就是指当x→∞时，limitf(x)存在，即limitf(x)＝C为某一常数。

y=e^x/(x+2)(x-1) 求垂直渐近线 (1) 先找出间断点，为x=-2和x=1 (2) 计算lim x→-2 y =lim x→-2 e^x/(x+2)(x-1) =∞ 同理，计算lim x→1 e^x/(x+2)(x-1)=∞ (3) 所以x=-2和x=1是y的垂直渐近线。

该情况所需具体条件如下：要找到函数的定义域，定义域是函数能够取值的范围。接下来需要寻找函数在定义域上的极限，函数在某个点的左极限和右极限都不存在或者有限的，这个点就是垂直渐近线的潜在位置。对于一个函数 ，其在某个点a处的极限不存在或者有限的，垂直渐近线的方程可以写为x等于a。