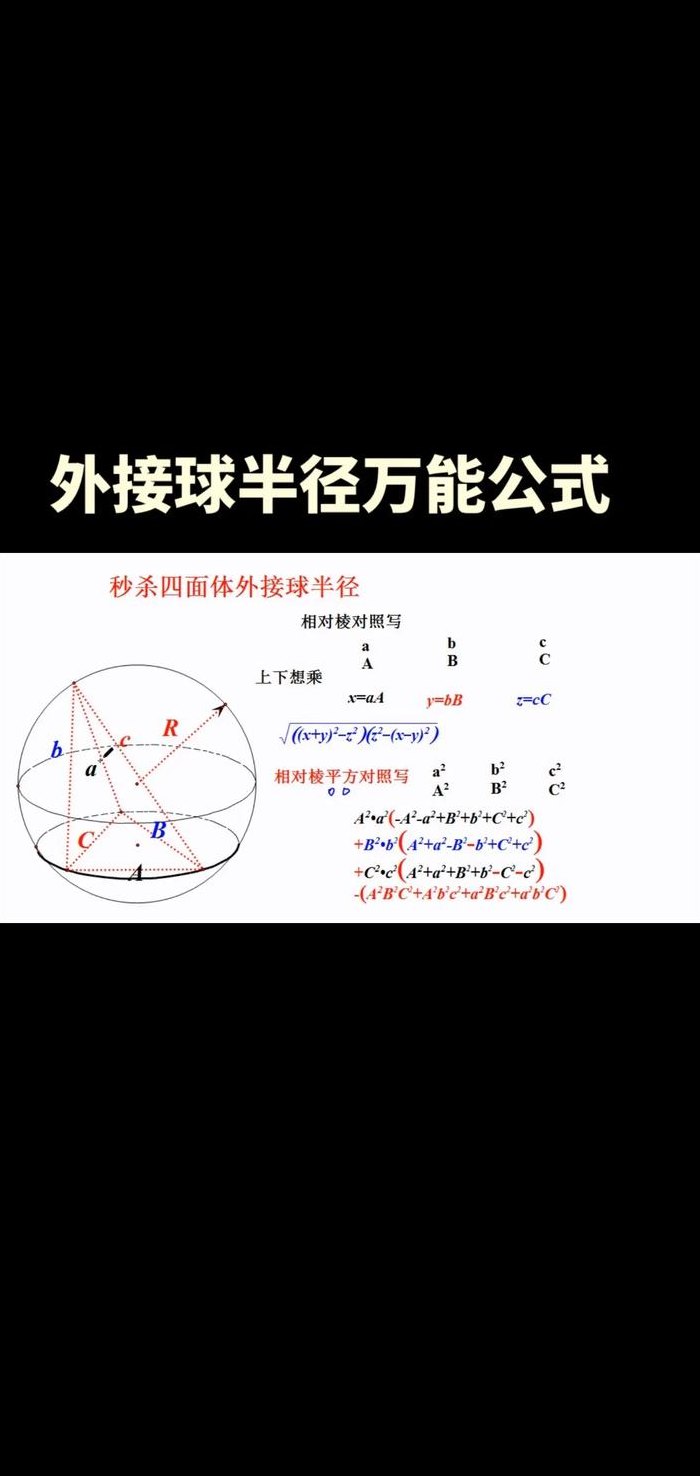
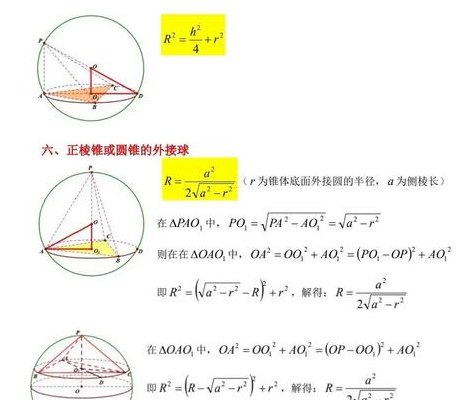
几何体外接球半径求法（常见几何体外接球秒杀公式）

外接球半径怎么求

1、求外接球的半径，可以按照以下方法来进行哦：使用公式法：对于某些特定的几何体，可以直接使用公式=R来计算外接球的半径，其中a和b是几何体的某些特定边长或尺寸，R就是外接球的半径啦。不过要注意，这个公式不是通用的，只适用于某些特定情况哦。

2、求外接球的半径公式：（a^2-b^2/3)=R。外接球意指一个空间几何图形的外接球，对于旋转体和多面体，外接球有不同的定义，广义理解为球将几何体包围，且几何体的顶点和弧面在此球上。正多面体各顶点同在一球面上，这个球叫做正多面体的外接球。

3、外接球的半径求法如下：求外接球的半径一般涉及两个主要步骤：找到球心和计算半径。要找到球心。对于一个外接球来说，其球心必然是三个对称轴的交点。对于一个长方体，其对称轴分别是面对角线、体对角线和棱边。因此，长方体的外接球的球心，就是体对角线的交点。要计算半径。

4、外接球半径万能公式：R=√[R_1^2+R_2^2- (L^2)/4]。若相互垂直的两凸多边形的外接圆半径分别为R_1，R_2，两外接圆公共弦长为L，则由两凸多边形顶点连接而成的几何体的外接球半径。方法：设A－BCD是正三棱锥，侧棱长为a，底面边长为b，则外接球的球心一定在这个三棱锥的高上。

5、对于正六面体（正立方体）：外接球半径（R）= a * √2 / 2 其中，a 表示正六面体的边长。 对于正四面体：外接球半径（R）= a * √6 / 4 其中，a 表示正四面体的边长。 对于正八面体：外接球半径（R）= a * √2 其中，a 表示正八面体的边长。

6、直接求法：首先将底面放在立体几何的xy平面上，然后用已知条件表示出四个顶点的坐标，之后通过圆的方程解出底面外心的为位置，然后连接外心和顶点，再用球心到四个顶点距离相等（到顶点和另一个底面上的顶点距离相等即可），从而求出外接球球心，然后就很容易得到半径。

常考外接球半径公式

外接球半径万能公式：R=√[R_1^2+R_2^2- (L^2)/4]。若相互垂直的两凸多边形的外接圆半径分别为R_1，R_2，两外接圆公共弦长为L，则由两凸多边形顶点连接而成的几何体的外接球半。外接球。

外接球半径万能公式：R=√[R_1^2+R_2^2- (L^2)/4]。若相互垂直的两凸多边形的外接圆半径分别为R_1，R_2，两外接圆公共弦长为L，则由两凸多边形顶点连接而成的几何体的外接球半径。

外接球半径的万能公式：设A-BCD为一个正三棱锥，侧棱长为a，底面边长为b。 外接球的球心必定位于三棱锥的高上。设高为AM，连接DM交BC于点E，连接AE，然后在面ADE内做侧棱AD的垂直平分线，交三棱锥的高AM于点O，点O即为外接球的球心。

外接球半径（R）= a * √6 / 4 其中，a 表示正四面体的边长。 对于正八面体：外接球半径（R）= a * √2 其中，a 表示正八面体的边长。 对于正二十面体：外接球半径（R）= a * √3 / 4 其中，a 表示正二十面体的边长。需要注意的是，这些公式是基于特定几何体的理想情况。

正棱锥模型：对于正棱锥，若其侧棱长度相等，则其外接球半径可通过正棱锥的高和底面边长计算得出。具体公式为：球半径 = (底面边长 / 2) * √((高 + 底面边长) / (高 - 底面边长))。

要计算半径。球心和长方体的一个顶点之间的距离就是半径。具体计算方法如下：设长方体的长、宽、高分别为a、b、c，那么外接球的半径R可以通过以下公式求得：R=√|（a^2+b^2+c^2）/2。

外接球半径的计算公式是什么?

1、外接球半径（R）= a * √6 / 4 其中，a 表示正四面体的边长。 对于正八面体：外接球半径（R）= a * √2 其中，a 表示正八面体的边长。 对于正二十面体：外接球半径（R）= a * √3 / 4 其中，a 表示正二十面体的边长。需要注意的是，这些公式是基于特定几何体的理想情况。

2、求外接球的半径公式：（a^2-b^2/3)=R。外接球意指一个空间几何图形的外接球，对于旋转体和多面体，外接球有不同的定义，广义理解为球将几何体包围，且几何体的顶点和弧面在此球上。正多面体各顶点同在一球面上，这个球叫做正多面体的外接球。

3、外接球半径万能公式：R=√[R_1^2+R_2^2- (L^2)/4]。若相互垂直的两凸多边形的外接圆半径分别为R_1，R_2，两外接圆公共弦长为L，则由两凸多边形顶点连接而成的几何体的外接球半。外接球。

4、外接球半径的计算公式为：R=（6）a/4。这里的外接球指的是一个空间几何图形的外接球，对于旋转体和多面体，外接球的定义有所不同。广义上，外接球是指能够包围几何体，并使几何体的顶点和弧面都位于该球面上的球。

5、要计算半径。球心和长方体的一个顶点之间的距离就是半径。具体计算方法如下：设长方体的长、宽、高分别为a、b、c，那么外接球的半径R可以通过以下公式求得：R=√|（a^2+b^2+c^2）/2。

6、外接球半径的万能公式：设A-BCD为一个正三棱锥，侧棱长为a，底面边长为b。 外接球的球心必定位于三棱锥的高上。设高为AM，连接DM交BC于点E，连接AE，然后在面ADE内做侧棱AD的垂直平分线，交三棱锥的高AM于点O，点O即为外接球的球心。

外接球的半径怎么求

求外接球的半径，可以按照以下方法来进行哦：使用公式法：对于某些特定的几何体，可以直接使用公式=R来计算外接球的半径，其中a和b是几何体的某些特定边长或尺寸，R就是外接球的半径啦。不过要注意，这个公式不是通用的，只适用于某些特定情况哦。

外接球半径万能公式：R=√[R_1^2+R_2^2- (L^2)/4]。若相互垂直的两凸多边形的外接圆半径分别为R_1，R_2，两外接圆公共弦长为L，则由两凸多边形顶点连接而成的几何体的外接球半径。方法：设A－BCD是正三棱锥，侧棱长为a，底面边长为b，则外接球的球心一定在这个三棱锥的高上。

外接球的半径求法如下：求外接球的半径一般涉及两个主要步骤：找到球心和计算半径。要找到球心。对于一个外接球来说，其球心必然是三个对称轴的交点。对于一个长方体，其对称轴分别是面对角线、体对角线和棱边。因此，长方体的外接球的球心，就是体对角线的交点。要计算半径。

求外接球的半径公式：（a^2-b^2/3)=R。外接球意指一个空间几何图形的外接球，对于旋转体和多面体，外接球有不同的定义，广义理解为球将几何体包围，且几何体的顶点和弧面在此球上。正多面体各顶点同在一球面上，这个球叫做正多面体的外接球。

几何体的内外接球的半径怎么求

求几何体的内外接球半径，需考虑几何体的具体类型。对于长方体，求解的关键在于求得其体对角线，体对角线即为球的直径。具体操作上，长方体的体对角线长度等于其长、宽、高的平方和的平方根。因此，球的半径就是体对角线长度的一半。对于直角四面体，其外接球的半径问题可以通过构造长方体来解决。

要看是什么几何体了，1，若为长方体的话只要想办法求出它的体对角线即为球体的直径。

外接球。边长为a的正四面体可以看成是边长是(√2/2)a的正方体截出来的，则其外接球直径是正方体边长的√3倍。内切球半径。

外接球半径（R）= a * √2 / 2 其中，a 表示正六面体的边长。 对于正四面体：外接球半径（R）= a * √6 / 4 其中，a 表示正四面体的边长。 对于正八面体：外接球半径（R）= a * √2 其中，a 表示正八面体的边长。

求外接球的半径，可以按照以下方法来进行哦：使用公式法：对于某些特定的几何体，可以直接使用公式=R来计算外接球的半径，其中a和b是几何体的某些特定边长或尺寸，R就是外接球的半径啦。不过要注意，这个公式不是通用的，只适用于某些特定情况哦。

...形ABC为正三角形,PA垂直于底面,PA=2,AB=2,求三棱锥外接球半径...

构建辅助图形：首先，正三棱锥的外接球问题可以通过补形的方式转化为求解长方体的外接球半径。补形后的长方体的三条边分别为三棱锥的棱长、高以及从顶点垂直于底面的距离。 计算长方体的对角线：已知长方体的三条边长后，可以计算其体对角线长度。体对角线即是外接球的直径。

到顶点和另一个底面上的顶点距离相等即可），从而求出外接球球心，然后就很容易得到半径。间接求法：球半径用等体积法，连接内切球球心和棱锥各顶点分割成若干三棱锥，则每个三棱锥体积为1/3底面积×R，全棱锥体积为1/3全面积×R；外接球则先考查任一侧面的三点外心的法。

设高为AM，连接DM交BC于E，连接AE，然后在面ADE内做侧棱AD的垂直平分线交三棱锥的高AM于O，则0就是外接球的球心，AO，DO是外接球的半径。

最后，将斜边长度代入勾股定理，并求出 r 的值即可。具体的，假设三棱锥的底面是一个正三角形，顶点坐标分别为（±a，0，0）和（0，±b，0），则三角形的斜边长度为 c=sqrt(a^2+b^2)，r 的值就是 OC 的长度，也就是 r=sqrt(c^2+h^2)，其中 h 是三棱锥的顶点到底面的距离。

解析：∵到PC是Rt△PAC和Rt△PBC的公共的斜边，记它的中点为O，则OA=OB=OP=OC=1/2 PC=1，即该三棱锥的外接球球心为O，半径为1。