杠杆原理（杠杆原理的定义）

杠杆的原理的原理是什么?

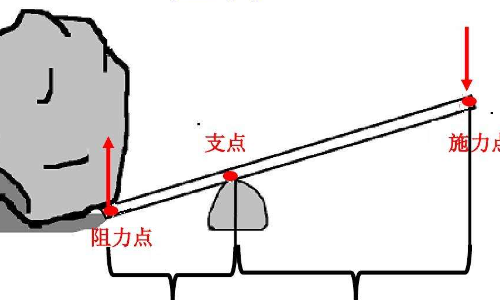
杠杆原理是作用在杠杆上的两个力矩（力与力臂的乘积）大小必须相等。即：动力×动力臂=阻力×阻力臂，用代数式表示为F1·L1=F2·L2。式中，F1表示动力，L1表示动力臂，F2表示阻力，L2表示阻力臂。因此要使杠杆达到平衡，动力臂是阻力臂的几倍，阻力就是动力的几倍。

杠杆原理公式：动力×动力臂=阻力×阻力臂，即：F1×L1=F2×L2。式中，F1表示动力，L1表示动力臂，F2表示阻力，L2表示阻力臂，杠杆原理也叫做“杠杆平衡条件”。要使杠杆平衡，作用在杠杆上的两个力（用力点、支点和阻力点）的大小跟它们的力臂成反比。

杠杆原理概述：杠杆原理是指通过支点，利用动力臂和阻力臂之间的力矩平衡关系，达到撬动重物或实现其他功能的目的。 支点的重要性：杠杆工作的基础是支点的选择。支点确定了力和力矩的作用位置，是杠杆运动的关键点。通过改变支点的位置，可以调整杠杆的工作效率和所需的力的大小。

杠杆原理称为杠杆平衡条件。杠杆又分称费力杠杆、省力杠杆和等臂杠杆，杠杆原理也称为“杠杆平衡条件”。要使杠杆平衡，作用在杠杆上的两个力矩（力与力臂的乘积）大小必须相等。即：动力×动力臂=阻力×阻力臂，用代数式表示为F1· L1=F2·L2。

杠杆原理表明，在杠杆平衡状态下，作用在杠杆两端的两个力矩相等。这两个力矩是由作用力与它们各自作用臂的乘积所组成。

杠杆原理定义：杠杆原理指的是动力乘以动力臂等于阻力乘以阻力臂，数学表达式为F1*L1=F2*L2。 杠杆概念扩展：杠杆最初特指财务杠杆，即企业使用借入资金进行投资以增加自有资金的收益。 财务杠杆应用：举例来说，一个公司如果自有资金不足，可以通过借款来补充，这样可以用借来的钱创造更多收益。

杠杆平衡的原理是什么

1、杠杆原理就是“杠杆平衡条件”。要使杠杆平衡，作用在杠杆上的两个力（动力和阻力）的大小跟它们的力臂成反比。动力×动力臂=阻力×阻力臂，用代数式表示为F1·L1=F2·L2。式中。F1表示动力，L1表示动力臂，F2表示阻力，L2表示阻力臂。

2、杠杆平衡的原理是杠杆定律。具体来说，就是杠杆在平衡状态下，作用在其上的所有力矩的总和应等于零。这就意味着，杠杆所受到的各种力量及其对应的力臂长度乘积的总和，必须保持平衡。换句话说，杠杆的平衡状态只有在满足力矩平衡的条件下才能实现。

3、杠杆平衡的原理，通常称为“杠杆平衡条件”，表述了要使杠杆保持平衡，作用在杠杆上的两个力（动力和阻力）的大小与它们的力臂成反比。这一原理可以用代数式F1·L1=F2·L2来表示，其中F1代表动力，L1代表动力臂，F2代表阻力，L2代表阻力臂。

4、杠杆平衡公式的原理是力矩平衡原理。它基于力矩的相等性来定义杠杆平衡状态。简单来说，就是当杠杆在力的作用下处于静止或匀速转动状态时，杠杆两端的力矩必须相等。具体原理的解释可以分为以下几个段落：基本概念理解 首先理解杠杆的平衡状态。

5、杠杆平衡的原理核心在于两个力矩的平衡，即动力乘以动力臂等于阻力乘以阻力臂，数学表达式为 F1· L1=F2·L2。这里的 F1代表动力，L1是动力臂，F2是阻力，L2是阻力臂。这意味着，如果动力臂是阻力臂的几倍，那么相应的阻力也需要是动力的几倍，才能保持杠杆的平衡。

6、杠杆又分称费力杠杆、省力杠杆和等臂杠杆，杠杆原理也称为“杠杆平衡条件”。要使杠杆平衡，作用在杠杆上的两个力矩（力与力臂的乘积）大小必须相等。即：动力×动力臂=阻力×阻力臂，用代数式表示为F1·L1=F2·L2。式中，F1表示动力，L1表示动力臂，F2表示阻力，L2表示阻力臂。

扛杆原理公式

1、杠杆原理公式：动力×动力臂=阻力×阻力臂，即：F1×L1=F2×L2。式中，F1表示动力，L1表示动力臂，F2表示阻力，L2表示阻力臂，杠杆原理也叫做“杠杆平衡条件”。要使杠杆平衡，作用在杠杆上的两个力（用力点、支点和阻力点）的大小跟它们的力臂成反比。

2、杠杆原理公式：动力×动力臂=阻力×阻力臂，用代数式表示为F1·l1=F2·l2。式中，F1表示动力，l1表示动力臂，F2表示阻力，l2表示阻力臂。从上式可看出，要使杠杆达到平衡，动力臂是阻力臂的几倍，阻力就是动力的几倍。杠杆又分成费力杠杆、省力杠杆和等臂杠杆，杠杆原理也称为“杠杆平衡条件”。

3、杠杆原理公式：功率×功率臂=阻力×阻力臂由代数公式F1·l1=f2·L2表示，其中F1表示功率，l1表示动力臂，f2表示阻力，L2表示阻力臂。由上式可以看出，要平衡杠杆，动力臂是阻力臂的数倍，阻力是动力臂的数倍。来自“on the balance of plane graphics”。

4、杠杆原理公式：动力×动力臂=阻力×阻力臂，用代数式表示为F1·L1=F2·L2，式中，F1表示动力，L1表示动力臂，F2表示阻力，L2表示阻力臂。从上式可看出，要使杠杆达到平衡，动力臂是阻力臂的几倍，阻力就是动力的几倍。来源于《论平面图形的平衡》。

杠杆原理是什么

1、杠杆原理公式：动力×动力臂=阻力×阻力臂，即：F1×L1=F2×L2。式中，F1表示动力，L1表示动力臂，F2表示阻力，L2表示阻力臂，杠杆原理也叫做“杠杆平衡条件”。要使杠杆平衡，作用在杠杆上的两个力（用力点、支点和阻力点）的大小跟它们的力臂成反比。

2、杠杆原理是作用在杠杆上的两个力矩（力与力臂的乘积）大小必须相等。即：动力×动力臂=阻力×阻力臂，用代数式表示为F1·L1=F2·L2。式中，F1表示动力，L1表示动力臂，F2表示阻力，L2表示阻力臂。因此要使杠杆达到平衡，动力臂是阻力臂的几倍，阻力就是动力的几倍。

3、杠杆原理是一种物理学的原理，它描述了一种情况下，通过支点，一个力可以通过杠杆放大或改变其力的大小和方向。杠杆原理的具体解释如下：杠杆的定义 杠杆是一个刚性物体，它可以围绕一个固定的点进行转动。这个支点将杠杆分为两个部分，一个是施力点，另一个是受力点。

4、杠杆原理是物理学中的力学定理，它指出要使杠杆平衡，作用在杠杆上的两个力矩（力与力臂的乘积）必须相等。这个原理可以用公式表示为F1·L1=F2·L2，其中F1是动力，L1是动力臂，F2是阻力，L2是阻力臂。换句话说，如果一个杠杆要达到平衡，那么动力臂是阻力臂的几倍，阻力就是动力的几倍。

杠杆原理简单概括

1、杠杆原理定义：杠杆原理指的是动力乘以动力臂等于阻力乘以阻力臂，数学表达式为F1*L1=F2*L2。 杠杆概念扩展：杠杆最初特指财务杠杆，即企业使用借入资金进行投资以增加自有资金的收益。 财务杠杆应用：举例来说，一个公司如果自有资金不足，可以通过借款来补充，这样可以用借来的钱创造更多收益。

2、杠杆原理的原因是基于力矩的平衡原理。杠杆原理是物理学中非常基础且重要的一条原理。它的核心思想可以概括为：在满足杠杆平衡的条件下，作用在杠杆上的力与其对应的力臂的乘积是相等的。这一原理的根源在于力矩的平衡原理。详细解释： 力矩平衡原理：这是杠杆原理的基础。

3、杠杆原理是作用在杠杆上的两个力矩（力与力臂的乘积）大小必须相等。即：动力×动力臂=阻力×阻力臂，用代数式表示为F1·L1=F2·L2。式中，F1表示动力，L1表示动力臂，F2表示阻力，L2表示阻力臂。因此要使杠杆达到平衡，动力臂是阻力臂的几倍，阻力就是动力的几倍。

4、在力学里，典型的 杠杆 （lever）是置放连结在一个支撑点上的硬棒，这硬棒可以绕着支撑点旋转。古希腊人将杠杆归类为简单机械，并且严谨地研究出杠杆的操作原理。某些杠杆能够将输入力放大，给出较大的输出力，这功能称为“杠杆作用”。杠杆的机械利益是输出力与输入力的比率。

5、物理杠杆知识点归纳1 杠杆原理亦称杠杆平衡条件。要使杠杆平衡，作用在杠杆上的两个力(动力点、支点和阻力点)的大小跟它们的力臂成反比。动力动力臂=阻力阻力臂，用代数式表示为F？ L1=W？L2。式中，F表示动力，L1表示动力臂，W表示阻力，L2表示阻力臂。