二进制与十六进制对应表（二进制与十六进制对应表图片）

十六进制和二进制的对应关系表

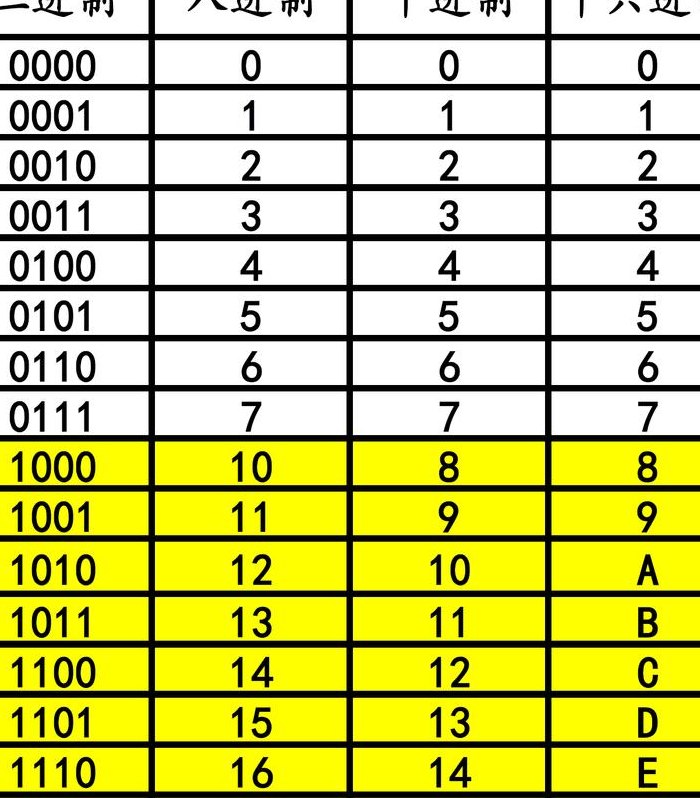
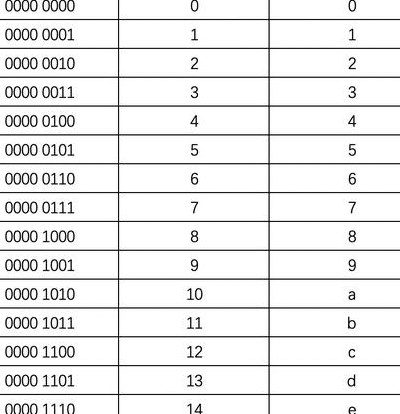
1、首先，先要看看十六位数的表示方法。二进制数与十六进制数之间的对应关系表，如下：二进制转换成十六进制的方法是，取四合一法，即从二进制的小数点为分界点，向左（或向右）每四位取成一位。

2、二进制和十六进制的对应关系如下图所示：十六进制对应的二进制数要比十进制数本身好记。你看，0~9十个符号和它们代表的数值当初是费了功夫才记住的，只是我们现在熟悉了而已；而二进制数字只需记住0、1两个符号而且它们就代表0和1。

3、F 1111 其中，A到F分别对应十进制的10到15。

4、位2进制数 刚好是从 0000 （零）到 1111 （十五），所以 二进制与十六进制数的互换极其简单： 二到十六 四位一并（不够补0）； 十六到二 一位拆四。

5、十六进制数转换为二进制数的过程涉及将每一位十六进制数分解为其对应的二进制数。

6、十六进制数和二进制数对应如下：十进制中转法：先将16进制数转为对应的十进制数，再将十进制数转为二进制。例如，16进制数12D.4A转为二进制，整数部分12D转换成0001 0010 1101，小数部分0.4A转换成0110 0101，最终拼接得到整体的二进制数0001 0010 1100110 0101。

二进制转十六进制怎么算?

1、二进制转十六进制，取四合一法，即从二进制的小数点为分界点，向左（或向右）每四位取成一位。具体方法如下。首先，先要看看十六位数的表示方法。

2、位2进制数 刚好是从 0000 （零）到 1111 （十五），所以 二进制与十六进制数的互换极其简单： 二到十六 四位一并（不够补0）； 十六到二 一位拆四。

3、二转十六的简单方法 8 4 2 1 权值相加法 要点： 1 将二进制数由低位到高位每 4 个1 节排开， 1111 2 在二进制数下面即可直接用加法写出十六进制的值 8421 ，上面在有 1 则添对应的权值为0则添0或不添。3　权值相加即得。

4、二进制转十六进制方法为：十六进制是取四合一，即从二进制的小数点为分界点，向左（或向右）每四位取成一位；组分好以后，对照二进制与十六进制数的对应表，将四位二进制按权相加，得到的数就是一位十六进制数，然后按顺序排列，小数点的位置不变，最后得到的就是十六进制数。

5、二进制转十六进制的方法是 将二进制数按每4位分成一组，不足4位的在左侧用0补齐，然后将每组转换为十六进制数，最后将所有转换后的十六进制数按顺序排列即可得到转换后的十六进制数。

6、进制转16进制怎么算，如下：二进制进位规则是“逢二进一”，借位规则是“借一当二”。二进制转16进制，只需将2进制数从右向左每四位一组合，每一个组合以一个十六进制数表示，(注意位数不足补0)。数一下这串数字一共多少个，然后把它们从右到左四个一组分好。

1到15的十进制、二进制和十六进制的值分别是多少?

1、转换为二进制是1110，而在十六进制中则为E，展示了数字在不同进制之间的直接对应。15的二进制形式是1111，而在十六进制中则为F，这展示了数字在十六进制中的表示方式。通过这些简单的例子，我们可以清晰地看到十进制数字在不同进制系统之间的转换规律，这对于理解计算机科学中的基本概念非常重要。

2、让我们来探讨一下1到15在不同进制下的表示方式。以十进制数1为例，它的八进制表示为1，十六进制表示为1，二进制表示为0001。十进制数2的八进制表示为2，十六进制表示为2，二进制表示为0010。以此类推，直到十进制数15，它的八进制表示为17，十六进制表示为F，二进制表示为1111。

3、1111 17 F 进制也就是进位制，是人们规定的一种进位方法。 对于任何一种进制---X进制，就表示某一位置上的数运算时是逢X进一位。 十进制是逢十进一，十六进制是逢十六进一，二进制就是逢二进一，以此类推，x进制就是逢x进位。

4、二进制和十六进制，八进制一样，都以二的幂来进位的。二进制的优点：数字装置简单可靠，所用元件少；只有两个数码0和1，因此它的每一位数都可用任何具有两个不同稳定状态的元件来表示；基本运算规则简单，运算操作方便。二进制的缺点：用二进制表示一个数时，位数多。

十六进制和二进制数的互换怎么做?

1、位2进制数 刚好是从 0000 （零）到 1111 （十五），所以 二进制与十六进制数的互换极其简单： 二到十六 四位一并（不够补0）； 十六到二 一位拆四。

2、进制多位数字母需要换算，换算方法：16进制数的第0位的权值为16的0次方，第1位的权值为16的1次方，第2位的权值为16的2次方？所以，在第N（N从0开始）位上，如果是是数 X （X 大于等于0，并且X小于等于 15，即：F）表示的大小为 X * 16的N次方。

3、首先，先要看看十六位数的表示方法。二进制数与十六进制数之间的对应关系表，如下：二进制转换成十六进制的方法是，取四合一法，即从二进制的小数点为分界点，向左（或向右）每四位取成一位。