正态分布密度曲线（正态分布密度曲线图）

标准正太分布的概率密度曲线是什么样子的。

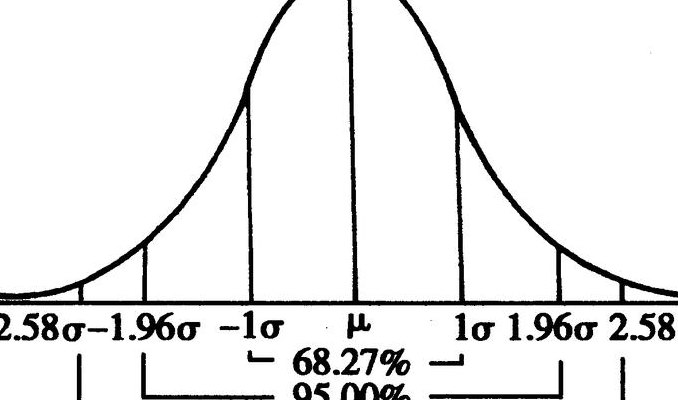
1、标准正态分布是一个在数学、物理及工程等领域都非常重要的概率分布，在统计学的许多方面有着重大的影响力。期望值μ=0，即曲线图象对称轴为Y轴，标准差σ=1条件下的正态分布，记为N(0，1)。

2、标准正态分布是指具有均值为0、标准差为1的正态分布。其概率密度函数为：f(x) = (1/√(2π)) * e^(-x^2/2)其中，x表示随机变量的取值，e是自然对数的底，π是圆周率。标准正态分布的概率密度函数曲线呈钟形，且对称于均值为0的直线。

3、正态曲线呈钟型，两头低，中间高，左右对称因其曲线呈钟形，因此人们又经常称之为钟形曲线。若随机变量X服从一个数学期望为μ、方差为σ^2的正态分布，记为N(μ，σ^2)。其概率密度函数为正态分布的期望值μ决定了其位置，其标准差σ决定了分布的幅度。

4、正态曲线 呈钟型，两头低，中间高，左右对称因其曲线呈钟形，因此人们又经常称之为钟形曲线。若随机变量X服从一个数学期望为μ、方差为σ2的正态分布，记为N(μ，σ2)。其概率密度函数为正态分布的期望值μ决定了其位置，其标准差σ决定了分布的幅度。

正态密度曲线微分方程和推导过程

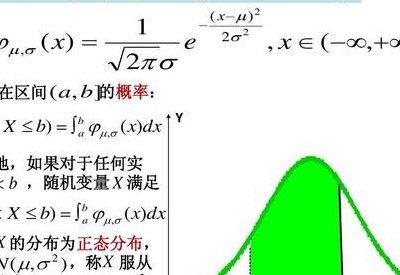
正态分布的概率密度函数表达式为：f(x)=1/(√(2π)*σ)e^[-(x-μ）＾2/(2σ^2)]，适用于x的取值范围从负无穷到正无穷，且σ大于零。其中，μ表示正态分布的均值，σ表示正态分布的标准差。分布函数F(x)定义为从负无穷到x的累积概率，即F(x)=∫(－∞，x]f(x)dx。

正态分布的概率密度函数是通过卡尔斯法拉公式推导得出的数学表达式。这个函数的精确形式如下：f(x)=1/√2πσexp[-(x-μ)^2/2σ^2]其中，μ表示正态分布的均值，σ表示标准差。这个函数的关键在于其描述了一个连续随机变量取值的概率密度。

正态分布的概率密度函数是通过一系列数学推导得到的。首先，我们从概率统计学的基本公理出发，假设一个连续随机变量的概率分布必须满足非负性和归一化条件。然后，通过对大量观测数据的分析，人们发现许多数据呈现出一种钟形曲线分布的特点，这就是正态分布。

通过最大化似然函数，我们得到[公式]，进一步推导得[公式]，其中[公式]。当[公式]和[公式]时，分别有[公式]和[公式]，这是柯西函数方程的解。最终，正态分布的概率密度函数公式为[公式]，并且通过规范化条件[公式]，我们得出[公式]。这个函数背后，隐藏着高斯分布的有趣历史。

正态密度曲线公式的分子不一定是一吗

是的。正态分布密度分布函数纵坐标值可以大于1的。因为密度函数的图像是钟形曲线，且曲线与x轴围成的面积等于1。当纵坐标高度比较高时，则钟形就比较细长，当纵坐标比较低时，钟形就比较胖了。只要与x轴围成的面积为1即可。正态分布曲线反映了随机变量的分布规律。

正态分布密度函数公式：f（x）=2/√2π/2σ^/（x-σ^2）。正态曲线呈钟型，两头低，中间高，左右对称因其曲线呈钟形，因此人们又经常称之为钟形曲线。由于一般的正态总体其图像不一定关于y轴对称，对于任一正态总体，其取值小于x的概率。只要会用它求正态总体在某个特定区间的概率即可。

这是由它的意义决定的。它=P{X=正无穷}就是X小于等于正无穷的概率，当然是100%。

概率分布密度函数f(x)是分布函数F(x)的导数，F(x)满足∫-∞，xf(x)dx=F(x).F(+∞)=实践中允许有误差。

标准正态分布的密度函数表达式为：\( \frac{1}{\sqrt{2\pi}}e^{-\frac{x^2}{2}} \)。这个公式描述了正态分布曲线的形状。正态曲线具有钟型特征，两头较低，中间较高，并且左右对称，这种图形也被称为钟形曲线。

正态分布的概率密度曲线呈钟形?

其中，x表示随机变量的取值，e是自然对数的底，π是圆周率。标准正态分布的概率密度函数曲线呈钟形，且对称于均值为0的直线。标准正态分布的分布函数Φ(x)定义如下：Φ(x) = ∫(-∞， x) (1/√(2π)) * e^(-t^2/2) dt 即，Φ(x)表示随机变量小于或等于x的概率。

曲线呈钟形：正态分布的概率密度函数曲线呈钟形，中间高，两边逐渐降低。这种形状使得正态分布在许多实际问题中具有广泛的适用性，如生物测量、质量控制等。

正态分布的概率密度函数公式：正态曲线呈钟型，两头低，中间高，左右对称因其曲线呈钟形，因此人们又经常称之为钟形曲线。算出平均值和标准差μ、σ，代入正态分布密度函数表达式：f(x) = exp{-(x-μ)/2σ}/[√(2π)σ]给定x值，即可算出f值。

正态曲线密度函数公式怎样求?

1、正态分布密度函数公式：f(x)=exp{-(x-μ）/2σ}/[√（2π）σ］。计算时，先算出平均值和标准差μ、σ，代入正态分布密度函数表达式，给定x值，即可算出f值。正态分布密度函数公式：正态曲线呈钟型，两头低，中间高，左右对称因其曲线呈钟形，因此人们又经常称之为钟形曲线。

2、正态分布的概率密度函数公式是f(x)=exp{-(x-μ)/2σ}/[√(2π)σ]。正态曲线呈现出钟型形态，两端较低，中间较高，左右对称，因此也被称为钟形曲线。若随机变量x遵循一个平均值为μ、方差为σ的正态分布，记作N（μ，σ）。

3、正态分布的概率密度函数表达式为：f(x)=1/(√(2π)*σ)e^[-(x-μ）＾2/(2σ^2)]，适用于x的取值范围从负无穷到正无穷，且σ大于零。其中，μ表示正态分布的均值，σ表示正态分布的标准差。分布函数F(x)定义为从负无穷到x的累积概率，即F(x)=∫(－∞，x]f(x)dx。

4、正态分布函数公式是P(x)=(2π)^(-1/2)*σ^(-1)*exp{[-(x-μ)^2]/(2σ^2)}。其中F(y)为Y的分布函数，F(x)为X的分布函数。其中μ为均数，σ为标准差。μ决定了正态分布的位置，与μ越近，被取到的概率就越大，反之越小。

5、标准正态分布密度函数：f(x)=(1/√2π)exp(-x^2/2)。而其中exp(-x^2/2)为e的-x^2/2次方，其定义域为（-∞，+∞），从概率密度表达式可以看出，f(x)是偶函数，即f(x)的图像关于y轴对称。

6、正态分布的概率密度函数公式是f(x)=exp{-(x-μ)/2σ}/[√(2π)σ]。正态曲线呈钟型，两头低，中间高，左右对称因其曲线呈钟形，因此人们又经常称之为钟形曲线。若随机变量x服从一个数学期望为、方差为0~2的正态分布，记为N（μ，02）。