指数函数的定义域（幂函数的定义域）

指数函数的定义域是什么

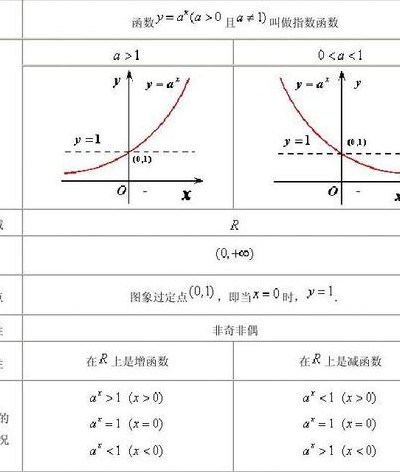
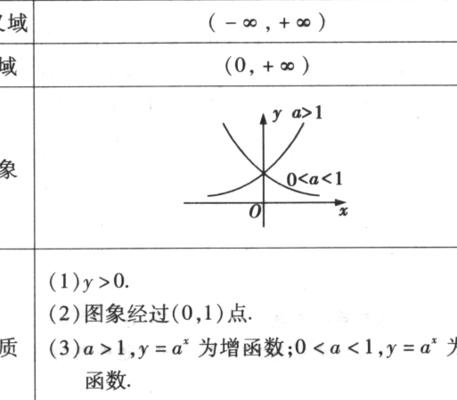
指数函数y=a^x(a0且a≠1)的定义域为R，值域为(0，+∞)，过定点(0，1)。当0a1时，在R上为减函数，当a1时是增函数。

指数函数的定义域为所有实数的集合，这里的前提是a大于0，对于a不大于0的情况，则必然使得函数的定义域不存在连续的区间，因此我们不予考虑。指数函数的值域为大于0的实数集合。函数图形都是下凹的。

一般地，y=ax函数(a为常数且以a0，a≠1)叫做指数函数，函数的定义域是 R ；，在指数函数的定义表达式中，在ax前的系数必须是数1，自变量x必须在指数的位置上，且不能是x的其他表达式，否则，就不是指数函数。

指数函数知识点总结

1、指数函数的概念知识点包括指数函数的概念、指数函数的结构特征、函数y＝af(x)的定义域、值域的求法、底数a必须大于0且不等于1的理由等部分。

2、高中数学指数函数知识点总结如下：指数函数是数学中的一种重要函数类型。指数函数可以用公式f(x)=e^x来表示，其中e是一个常数，约等于718。e^x函数的导数是指在每个点上函数的斜率或变化率。

3、指数函数有特定的图像与性质。当底数a1时，底数越大函数值增长越快，图像越靠近y轴。当底数0a1时，a越小图像越靠近y轴。

4、知识点定义来源和讲解：指数函数是数学中的一种重要函数类型。指数函数可以用公式f(x) = e^x来表示，其中e是一个常数，约等于718。e^x函数的导数是指在每个点上函数的斜率或变化率。

有关指数函数的定义域

1、指数函数是重要的基本初等函数之一。一般地，y=ax函数(a为常数且以a0，a≠1)叫做指数函数，函数的定义域是R。

2、指数函数的概念：一般地，函数叫做指数函数，其中x是自变量，函数的定义域为R。注意：指数函数的底数的取值范围，底数不能是负数、零和1。

3、指数函数的定义域为所有实数的集合，这里的前提是a大于0，对于a不大于0的情况，则必然使得函数的定义域不存在连续的区间，因此我们不予考虑。指数函数的值域为大于0的实数集合。函数图形都是下凹的。

4、一般地，函数（a0，且a≠1）叫做对数函数，也就是说以幂（真数）为自变量，指数为因变量，底数为常量的函数，叫对数函数。值域：实数集R，显然对数函数无界。定点：函数图像恒过定点(1，0)。