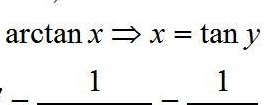正切函数的导数（正切函数的导数值）

正切函数的导数是什么?

arcsinx的导数是：y=1/cosy=1/√[1-(siny)]=1/√(1-x)，此为隐函数求导。

函数y=f（x）在x0点的导数f（x0）的几何意义，表示函数曲线在点P0（x0，f（x0））处的切线的斜率（导数的几何意义是该函数曲线在这一点上的切线斜率）。

其具体过程是：(tanx)′=(sinx/cosx)′=[(sinx)′cosx-sinx·(cosx)′]/cos^2x=[cos^2x+sin^2x]/cos^2x=1/cos^2x=sec^2x。即tanx求导结果为sec^2x。

正切函数的导数是(secx)^2；导数做好函数的局部性质。一个函数在某一点的导数描述了这个函数在这一点附近的变化率。如果函数的自变量和取值都是实数的话，函数在某一点的导数就是该函数所代表的曲线在这一点上的切线斜率。

在Rt△ABC中，如果锐角A确定，那么角A的对边与邻边的比值随之确定，这个比叫做角A的正切，记作tanA。(tanx)=1/cosx=secx=1+tanx。tanx求导的结果是secx，可把tanx化为sinx/cosx进行推导。

arcsinx的导数

arcsinx的导数是：y=1/cosy=1/√[1-(siny)]=1/√(1-x)，此为隐函数求导。

arcsinx的导数是1/√（1-x﹚，而arccosx=π/2-arcsinx，那么对arccosx求导，y=-1/√(1-x)。

arcsinx的导数是：y=1/cosy=1/√[1-(siny)]=1/√(1-x)； arccosx的导数：-1/√（1-x） 扩展资料 arccosx的导数解答过程如下：（1）y=arccosx则cosy=x。

arcsinx的导数(arcsinx)=1/根号（1-x^2）。设y=arcsinx∈[-π/2，π/2]，则x=siny ，1=（cosy)*y ，y=1/cosy=1/根号（1-sin^2y)=1/根号（1-x^2）。

正切函数导数为多少?

1、函数y=f（x）在x0点的导数f（x0）的几何意义，表示函数曲线在点P0（x0，f（x0））处的切线的斜率（导数的几何意义是该函数曲线在这一点上的切线斜率）。

2、正切函数的导数是(secx)^2；导数做好函数的局部性质。一个函数在某一点的导数描述了这个函数在这一点附近的变化率。如果函数的自变量和取值都是实数的话，函数在某一点的导数就是该函数所代表的曲线在这一点上的切线斜率。

3、其具体过程是：(tanx)′=(sinx/cosx)′=[(sinx)′cosx-sinx·(cosx)′]/cos^2x=[cos^2x+sin^2x]/cos^2x=1/cos^2x=sec^2x。即tanx求导结果为sec^2x。

4、tan的导数是secx。tanx求导的结果是secx，可把tanx化为sinx/cosx进行推导。求导的定义：当自变量的增量趋于零时，因变量的增量与自变量的增量之商的极限；在一个函数存在导数时，称这个函数可导或者可微分。

5、反正切函数的导数公式：1/1+x。

正切函数怎么求导数?

1、+(cotx)^2=(cscx)^2。倒数关系：sinxcscx=1，cosx.secx=1，tanxcotx=1。

2、通过微分可以得到正切函数的导数公式：（tanx）=（y/x）=（yx- y）/x^2。根据三角函数的性质，我们知道sin（x）=y/r（其中r是直角三角形的斜边长度），因此y=cos（x）sin（x）。

3、其具体过程是：(tanx)′=(sinx/cosx)′=[(sinx)′cosx-sinx·(cosx)′]/cos^2x=[cos^2x+sin^2x]/cos^2x=1/cos^2x=sec^2x。即tanx求导结果为sec^2x。

4、正切求导公式是(tanx)=secx*secx。求导是数学计算中的一个计算方法，它的定义就是，当自变量的增量趋于零时，因变量的增量与自变量的增量之商的极限。在一个函数存在导数时，称这个函数可导或者可微分。