最小的有理数（最小的有理数是0对不对）

最小的有理数是多少

可见没有最小的有理数，但是有绝对值最小的有理数。

最小有理数是1。 有理数：有理数是可以表示为两个整数的比值的数。有理数包括整数、分数和小数。 理数的比较：在数轴上，有理数可以按照大小进行比较。两个有理数可以通过比较分子和分母的大小来确定大小关系。

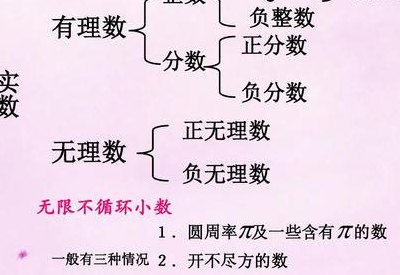
没有最小的有理数。正整数，0，负整数统称整数；正分数和负数统称分数，整数和分数统称有理数，所以没有最小的有理数。有理数集可以用大写黑正体符号Q代表。但Q并不表示有理数，有理数集与有理数是两个不同的概念。

有理数中最小的正整数是

1、最小的正整数是1。比0大的数叫正数，且无小数为整数，满足条件的最小值为1。正数与负数表示意义相反的量。

2、最小的正整数是（1），最大的负整数是（-1）。整数（integer）就是像-3，-2，-1，0，1，2，3，10等这样的数。整数的全体构成整数集，整数集是一个数环。在整数系中，零和正整数统称为自然数。

3、最小的非负整数是0。有理数中，最小的正整数是1，最大的负整数是-1，最大的非正数是0。

最小的有理数

1、没有最小的有理数，正整数，0，负整数统称整数；正分数和负数统称分数。整数和分数统称有理数。所以没有最小的有理数。有理数集可以用大写黑正体符号Q代表。但Q并不表示有理数，有理数集与有理数是两个不同的概念。

2、可见没有最小的有理数，但是有绝对值最小的有理数。

3、没有最小的有理数。正整数，0，负整数统称整数；正分数和负数统称分数，整数和分数统称有理数，所以没有最小的有理数。有理数集可以用大写黑正体符号Q代表。但Q并不表示有理数，有理数集与有理数是两个不同的概念。

4、最小的有理数是0。有理数是整数和分数的统称，所以最小的有理数当然是0了。当然，这只是从理论上来说的，实际上在某些情况下，最小的有理数可能不存在，例如在负有理数中，负数之间没有有理数可以取最小值。

5、最小的有理数是没有最小的有理数。不存在最小的有理数。

6、没有最小的有理数。有理数为整数（正整数、0、负整数）和分数的统称。正整数和正分数合称为正有理数，负整数和负分数合称为负有理数。因而有理数集的数可分为正有理数、负有理数和零。

最小的有理数是什么?

1、可见没有最小的有理数，但是有绝对值最小的有理数。

2、最小有理数是指在有理数集合中最小的那个数。由于有理数可以无限地向左延伸，所以最小有理数是负无穷大。 数轴上的有理数：数轴是一条直线，用来表示所有实数。

3、最小的有理数是0。有理数是整数和分数的统称，所以最小的有理数当然是0了。当然，这只是从理论上来说的，实际上在某些情况下，最小的有理数可能不存在，例如在负有理数中，负数之间没有有理数可以取最小值。

4、没有最小的有理数。正整数，0，负整数统称整数；正分数和负数统称分数，整数和分数统称有理数，所以没有最小的有理数。有理数集可以用大写黑正体符号Q代表。

5、没有最小的有理数。有理数为整数（正整数、0、负整数）和分数的统称。正整数和正分数合称为正有理数，负整数和负分数合称为负有理数。因而有理数集的数可分为正有理数、负有理数和零。