指数分布的期望和方差（六个常见分布的期望和方差）

X~e(λ)期望和方差是多少?

指数分布的参数为λ，则指数分布的期望为1/λ，方差为(1/λ)的平方。

其中期望是E(X)=1/λ，方差是D(X)=1/λ。

指数分布的期望：E（X）=1/λ。指数分布的方差：D（X）=Var（X）=1/λ。指数分布与分布指数族的分类不同，后者是包含指数分布作为其成员之一的大类概率分布，也包括正态分布，二项分布，伽马分布，泊松分布等等。

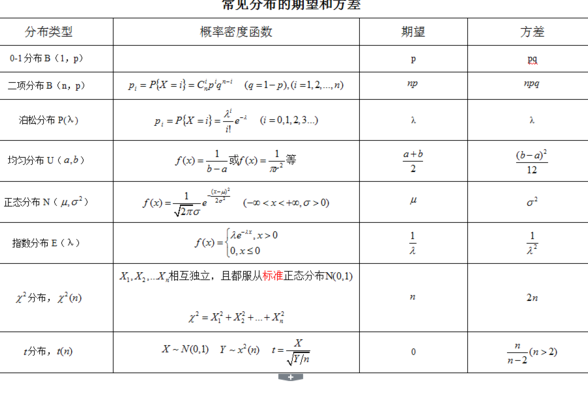
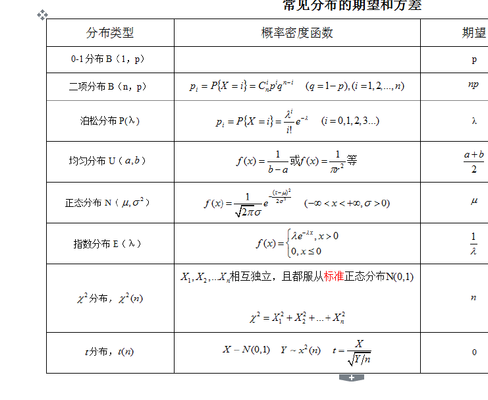
八大常见分布的期望和方差如下：0-1分布：E(X)=p，D(X)=p(1-p)。二项分布B(n，p)：P(X=k)=C(k\n)p^k·(1-p)^(n-k)，E(X)=np，D(X)=np(1-p)。泊松分布X~P(X=k)=(λ^k/k！)·e^-λ，E(X)=λ，D(X)=λ。

X~e(λ)=Γ(λ，1)，Y~e(λ)=Γ(λ，1)，根据Γ分布的性质有，X+Y~=Γ(λ，2)。随机过程中，任何时刻的取值都为随机变量，如果这些随机变量服从同一分布，并且互相独立，那么这些随机变量是独立同分布。

其中，E(X) 是随机变量 X 的期望（均值）。需要注意的是，方差是衡量随机变量离其期望值的平均偏离程度的统计量。方差的平方根称为标准差，标准差提供了对数据分布的更直观理解。这些公式适用于一般的随机变量，但对于特殊的分布（如正态分布、泊松分布等），还可以使用相应的公式来计算期望和方差。

指数分布的期望是什么?方差又是什么?

1、指数分布的期望是1/，方差是1/^2。指数分布是一种连续概率分布，通常用于描述事件发生的时间间隔，例如放射性衰变、电话呼叫到达时间间隔等。在指数分布中，参数表示单位时间内事件发生的平均次数，也称为事件的发生率。

2、期望值：方差：指数分布可以用来表示独立随机事件发生的时间间隔，比如旅客进机场的时间间隔，在排队论中，一个顾客接受服务的时间长短（等待时间等）也可以用指数分布来近似。

3、指数分布的期望：E（X）=1/λ。指数分布的方差：D（X）=Var（X）=1/λ。指数分布与分布指数族的分类不同，后者是包含指数分布作为其成员之一的大类概率分布，也包括正态分布，二项分布，伽马分布，泊松分布等等。

4、以1/θ为参数的指数分布，期望是θ，方差是θ的平方 这是同济大学4版概率论的说法。

5、指数分布，可以用来表示独立随机事件发生的时间间隔。指数分布的参数为λ，则指数分布的期望为1/λ，方差为(1/λ)的平方。

6、指数分布的期望和方差是描述该分布特性的重要统计量。指数分布是一种连续概率分布，常用于描述事件发生的时间间隔，如无线电信号到达的间隔时间、电话呼叫之间的时间间隔等。指数分布的一个重要特征是它的无记忆性，即事件之间的时间间隔是相互独立的，不受之前事件发生的影响。

指数分布的期望和方差是什么?

1、期望值：方差：指数分布可以用来表示独立随机事件发生的时间间隔，比如旅客进机场的时间间隔，在排队论中，一个顾客接受服务的时间长短（等待时间等）也可以用指数分布来近似。

2、指数分布的期望是1/，方差是1/^2。指数分布是一种连续概率分布，通常用于描述事件发生的时间间隔，例如无线电波到达接收机的时间间隔、网站访问者的到达间隔等。在指数分布中，参数表示单位时间内事件发生的平均次数，即事件的平均到达率。

3、指数分布，可以用来表示独立随机事件发生的时间间隔。指数分布的参数为λ，则指数分布的期望为1/λ，方差为(1/λ)的平方。