三角函数值大全表图（三角函数值大全表图 表格）

正弦余弦函数公式

1、三角函数正弦余弦公式大全：一 . 三角函数正弦余弦公式 正弦sin=对边比斜边、余弦cos=邻边比斜边、正切tan=对边比邻边、余切cot=邻边比对边 。

2、正弦定理：a/sinA=b/sinB=c/sinC=2R 余弦定理：cos A=(b+c-a)/2bc。正余弦定理指正弦定理和余弦定理，是揭示三角形边角关系的重要定理，直接运用它可解决三角形的问题，若对余弦定理加以变形并适当移于其它知识，则使用起来更为方便、灵活。

3、三角函数正弦公式为：sin(A) = 对边 / 斜边，余弦公式为：cos(A) = 邻边 / 斜边。正弦公式 正弦公式是 sin(x) = 对边 / 斜边，也可以表示为 sin(x) = b / c。

4、假如有一个直角三角形 ABC，其中 a、b 是直角边，c 是斜边。正弦(sin)等于对边比斜边；sinA=a/c；余弦(cos)等于邻边比斜边；cosA=b/c；正切(tan)等于对边比邻边；tanA=a/b。

5、公式如下：1/sinx=cscx 1/cosx=secx 对于任意一个实数x都对应着唯一的角（弧度制中等于这个实数），而这个角又对应着唯一确定的正弦值sinx，这样，对于任意一个实数x都有唯一确定的值sinx与它对应，按照这个对应法则所建立的函数，表示为y=sinx，叫做正弦函数。

三角函数值对照是什么?

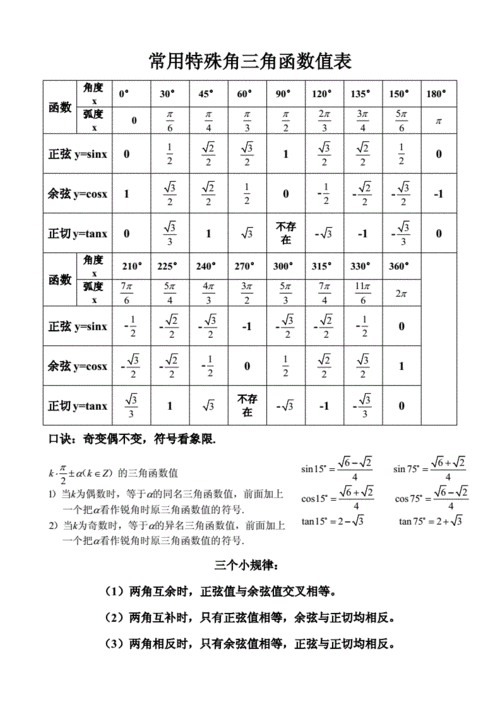
1、sin0°=0；sin90°=1；sin180°=0；sin270°=-1；sin360°=0；cos0°=1；cos90°=0；cos180°=-1；cos270°=0；cos360°=1；tan0°=0；tan90°=1；tan180°=0；tan360°=0；tan270°不存在，270不是tan函数的定义域。

2、三角函数值如下：三角函数是数学中属于初等函数中的超越函数的一类函数。它们的本质是任意角的集合与一个比值的集合的变量之间的映射。通常的三角函数是在平面直角坐标系中定义的，其定义域为整个实数域。另一种定义是在直角三角形中，但并不完全。

3、是数学中属于初等函数中的超越函数的一类函数。它们的本质是任意角的集合与一个比值的集合的变量之间的映射。通常的三角函数是在平面直角坐标系中定义的，其定义域为整个实数域。另一种定义是在直角三角形中，但并不完全。

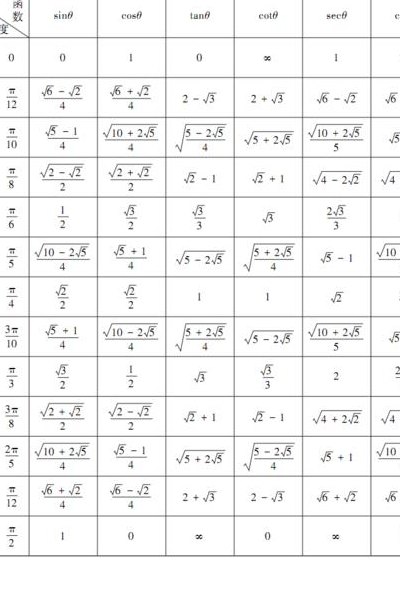
4、特殊角度的三角函数值对照表如下：10到360度三角函数值表 反三角函数值表 三角函数 常见的三角函数包括正弦函数、余弦函数和正切函数。在航海学、测绘学、工程学等其他学科中，还会用到如余切函数、正割函数、余割函数、正矢函数、余矢函数、半正矢函数、半余矢函数等其他的三角函数。

5、三角函数表如下：三角函数的本质是任何角的集合与一个比值的集合的变量之间的映射。通常的三角函数是在平面直角坐标系中定义的。其定义域为整个实数域。另一种定义是在直角三角形中，但并不完全。现代数学把它们描述成无穷数列的极限和微分方程的解，将其定义扩展到复数系。

常见三角函数值表是什么?

三角函数表如下：三角函数的本质是任何角的集合与一个比值的集合的变量之间的映射。通常的三角函数是在平面直角坐标系中定义的。其定义域为整个实数域。另一种定义是在直角三角形中，但并不完全。现代数学把它们描述成无穷数列的极限和微分方程的解，将其定义扩展到复数系。

初中常用的三角函数有正弦函数、余弦函数和正切函数等等，接下来分享具体的三角函数值表，供参考。

常见三角函数值：sin0=sin0°=0 cos0=cos0°=1 tan0=tan0°=0sin15=0.650 sin15°=0.259 cos15=-0.759；cos15°=0.966 tan15=-0.855；tan15°=0.268 sin30°=1/2 cos30°=0.866 判断三角函数值的符号 记忆口诀是：奇变偶不变，符号看象限。

完整初中三角函数值表如下图所示：常见的三角函数包括正弦函数、余弦函数和正切函数。在航海学、测绘学、工程学等其他学科中，还会用到如余切函数、正割函数、余割函数、正矢函数、余矢函数、半正矢函数、半余矢函数等其他的三角函数。

°，45°，60°这三个角的正弦值和余弦值的共同点是：分母都是2，若把分子都加上根号，则被开方数就相应地变成了1，2，3．正切的特点是将分子全部都带上根号，令分母值为3，则相应的被开方数就是3，9，27。

在高中阶段的三角内容是三角学的主体部分，包括解斜三角形、三角函数、反三角函数和简单的三角方程。无论是从内容上看，还是从思考问题的方法上看，前一部分都是后一部分的重要基础，掌握锐角三角函数的概念和解直角三角形的方法，是学习三角函数和解斜三角形的重要准备。

初中常见的三角函数值表

1、初中常用的三角函数有正弦函数、余弦函数和正切函数等等，接下来分享具体的三角函数值表，供参考。

2、完整初中三角函数值表如下图所示：常见的三角函数包括正弦函数、余弦函数和正切函数。在航海学、测绘学、工程学等其他学科中，还会用到如余切函数、正割函数、余割函数、正矢函数、余矢函数、半正矢函数、半余矢函数等其他的三角函数。

3、°，45°，60°这三个角的正弦值和余弦值的共同点是：分母都是2，若把分子都加上根号，则被开方数就相应地变成了1，2，3．正切的特点是将分子全部都带上根号，令分母值为3，则相应的被开方数就是3，9，27。

常用角的三角函数值是多少度?

°：sinα=0，cosα=1，tanα=0。

三角函数的本质是任何角的集合与一个比值的集合的变量之间的映射。通常的三角函数是在平面直角坐标系中定义的。其定义域为整个实数域。另一种定义是在直角三角形中，但并不完全。现代数学把它们描述成无穷数列的极限和微分方程的解，将其定义扩展到复数系。

零度九十度，斜线z形连。端点均为零，余下竖横填。判断三角函数值的符号 记忆口诀是：奇变偶不变，符号看象限。①当k是偶数时，得到α的同名函数值，即函数名不改变。②当k是奇数时，得到α相应的余函数值，即sin→cos；cos→sin；tan→cot，cot→tan。

°的三角函数如下图：常见的三角函数包括正弦函数、余弦函数和正切函数。在航海学、测绘学、工程学等其他学科中，还会用到如余切函数、正割函数、余割函数、正矢函数、余矢函数、半正矢函数、半余矢函数等其他的三角函数。不同的三角函数之间的关系可以通过几何直观或者计算得出，称为三角恒等式。

正弦：sin0°=sin180°=sin360°=0，sin90°=1，sin270°=-1 余弦：cos0°=cos360°=1，cos90°=cos270°=0，cos180°=-1 正切：tan0°=tan180°=tan360°=0，tan90°和tan270°无意义。

°，45°，60°这三个角的正弦值和余弦值的共同点是：分母都是2，若把分子都加上根号，则被开方数就相应地变成了1，2，3．正切的特点是将分子全部都带上根号，令分母值为3，则相应的被开方数就是3，9，27。