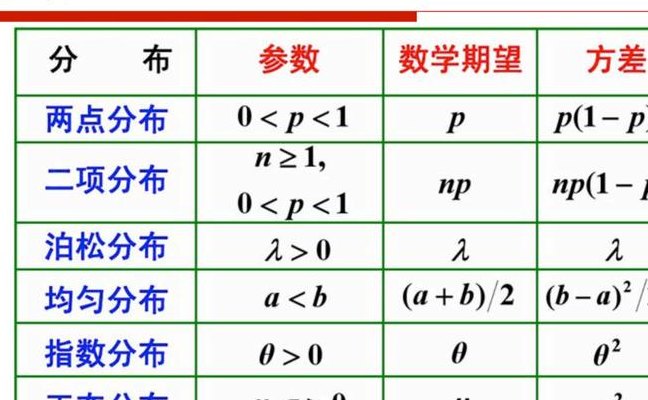
概率密度函数（概率密度函数和概率的关系）

随机变量的概率密度函数

Y的分步为：P（Y =x) = P(-ln X = x) = P(X = e^(-x)) = 1-e^(-x).因此密度函数为：f(x) = (1-e^(-x)) = e^(-x).名词解释：密度函数 对于一维实随机变量X，设它的累积分布函数是FX(x)。

随机变量X在区间(1，7)上服从均匀分布，也就是说P(1X7)=1，P(X≤1)=0，P(X≥7)=0。所以概率P(0.5X6)=概率P(1X6)=（6-1）/（7-1）=5/6。

随机变量的密度函数是描述随机变量概率分布的函数。密度函数通常用f(x)表示，其中x为随机变量的取值。对于连续型随机变量，密度函数定义了在不同取值范围内的概率密度。具体而言，对于一个连续型随机变量X，其密度函数f(x)满足以下性质：非负性：对于所有的x，f(x)≥ 0。

离散随机变量的密度函数：a. 伯努利分布：伯努利分布的密度函数是 P(X = x) = p^x * (1-p)^(1-x)，其中p是成功的概率，x可以是0或1。

由于随机变量X服从均匀分布，其概率密度函数为f_x(x) = 1/(2-(-2)) = 1/4，因此，我们可以根据公式f_y(y) = f_x(x) * |x|计算出Y的概率密度函数。所以，Y的概率密度函数为：f_y(y) = f_x(x) * |x| = 1/4 * |x|现在我们来计算Y的概率密度函数在区间[0， 8]内的值。

概率密度函数怎么求?

D(aX+bY)=+aD(X)+bD(Y)X 服从正态分布，即X~N(μ，σ^2)，则E(x)=μ，D(X)=σ^2 D（x）=0.6，D（y）=2 D(3X-Y)=9D(x)+D(Y）=9 ×0.6+2=4。

Y的概率密度函数为 f(x)= e^(-x) x≥0 0 其他 利用和的分布公式可知，Z的概率密度函数为 g(y)=∫R p(x)f(y-x)dx =0 y≤0 ∫[0，y]e^(x-y)dx=1-e^(-y) 01 也就是Z的概率密度是个分段函数。

求概率密度的方法：则X为连续型随机变量，称f(x)为X的概率密度函数，简称为概率密度。单纯的讲概率密度没有实际的意义，它必须有确定的有界区间为前提。可以把概率密度看成是纵坐标，区间看成是横坐标，概率密度对区间的积分就是面积，而这个面积就是事件在这个区间发生的概率，所有面积的和为1。

求谁不积谁（求X概率密度就积y)，不积先定限，限内画条线，先交为下限，后交为上限。先求Y的边缘概率密度了，联合概率密度与边缘概率密度的商就是条件概率密度。X的边缘分布的密度函数fX(x)=∫(-∞，∞)f(x，y)dy=∫(0，x)3xdy=3x，0x1fX(x)=0，x。

解：本题利用了联合概率密度的性质和和的分布公式求解。

随机变量的概率密度函数是什么?

1、连续型随机变量的概率密度函数（在不至于混淆时可以简称为密度函数）是一个描述这个随机变量的输出值，在某个确定的取值点附近的可能性的函数。而随机变量的取值落在某个区域之内的概率则为概率密度函数在这个区域上的积分。当概率密度函数存在的时候，累积分布函数是概率密度函数的积分。

2、随机变量X服从区间(2，4)上的均匀分布，求出X的概率密度fx=1/ (2＜x＜4) 其它处为0.从而Y=X2的分布函数是Fy =P (Y小于等于y)=P (x2小于等于y)。x2的取值是4到1当y小于等于4时，P=0.当y大于等于16时，P=1。

3、随机数据的概率密度函数：表示瞬时幅值落在某指定范围内的概率，因此是幅值的函数。它随所取范围的幅值而变化。密度函数f(x) 具有下列性质：（1）f(x)≧0；(2) ∫f(x)d(x)=1；（3）常见定义 对于一维实随机变量X，设它的累积分布函数是FX(x)。

4、随机变量X在区间(1，7)上服从均匀分布，也就是说P(1X7)=1，P(X≤1)=0，P(X≥7)=0。所以概率P(0.5X6)=概率P(1X6)=（6-1）/（7-1）=5/6。

随机变量的概率密度函数怎么求?

由此可得，a * b * c = 1。根据上述两个方程，我们可以得出a，b，c的取值为a = 1，b = 1，c = 1。接下来，我们求解概率密度函数。概率密度函数可以通过对分布函数求偏导数来获得。

Y的取值为[-1，1]， 先求分布，然后求导获得密度。

代入公式。在[a，b]上的均匀分布，期望=(a+b)/2，方差=[(b-a)^2]/2。代入直接得到结论。

随机变量的概率密度函数可以通过以下公式求得：f(x)=lim[1/(b-a) * P(a X = b)] 其中，a和b是区间端点，P(a X = b)是在该区间内取值的概率。需要注意的是，概率密度函数应该满足以下条件：(1) f(x) = 0 在整个定义域内；(2) ∫f(x) dx = 1。

概率的密度函数是什么?

概率密度为1/（2a）。概率密度等于一段区间(事件的取值范围)的概率除以该段区间的长度，它的值是非负的，可以很大也可以很小。单纯的讲概率密度没有实际的意义，它必须有确定的有界区间为前提。

概率密度函数为：f(x)二者的关系为：f(x) = dF(x)/dx 即：密度函数f 为分布函数 F 的一阶导数。或者分布函数为密度函数的积分。定义分布函数，是因为在很多情况下，我们并不想知道在某样东西在某个特定的值的概率，顶多想知道在某个范围的概率，于是，就有了分布函数的概念。

密度函数是一段区间的概率除以区间长度，值为正数，可大可小；而分布函数则是可以使用数学分析方法研究随机变量的一种曲线。密度函数一般只针对连续型变量，而分布函数则是既针对连续型也针对离散型随机变量。求解分布函数的时候要进行分类讨论和定积分计算，求解密度函数的时候需要进行求导。

概率密度函数是什么?

1、概率密度为1/（2a）。概率密度等于一段区间(事件的取值范围)的概率除以该段区间的长度，它的值是非负的，可以很大也可以很小。单纯的讲概率密度没有实际的意义，它必须有确定的有界区间为前提。

2、在数学中，连续型随机变量的概率密度函数（在不至于混淆时可以简称为密度函数）是一个描述这个随机变量的输出值，在某个确定的取值点附近的可能性的函数。而随机变量的取值落在某个区域之内的概率则为概率密度函数在这个区域上的积分。当概率密度函数存在的时候，累积分布函数是概率密度函数的积分。

3、概率密度函数：在数学中，连续型随机变里的概率密度函数（在不至于混淆时可以简称为密度函数）是一个描述这个随机变里的输出值，在某个确定的取值点附近的可能性的函数。公式：其中入0是分布的一个参数，常被称为率参数(rate par ameter)。即每单位时间内发生某事件的次数。指数分布的区间是[o， oo)。

4、密度函数是一段区间的概率除以区间长度，值为正数，可大可小；而分布函数则是可以使用数学分析方法研究随机变量的一种曲线。密度函数一般只针对连续型变量，而分布函数则是既针对连续型也针对离散型随机变量。求解分布函数的时候要进行分类讨论和定积分计算，求解密度函数的时候需要进行求导。

5、概率密度函数为：f(x)二者的关系为：f(x) = dF(x)/dx 即：密度函数f 为分布函数 F 的一阶导数。或者分布函数为密度函数的积分。定义分布函数，是因为在很多情况下，我们并不想知道在某样东西在某个特定的值的概率，顶多想知道在某个范围的概率，于是，就有了分布函数的概念。