有多少个三角形（第n个图形中有多少个三角形）

有多少个三角形?

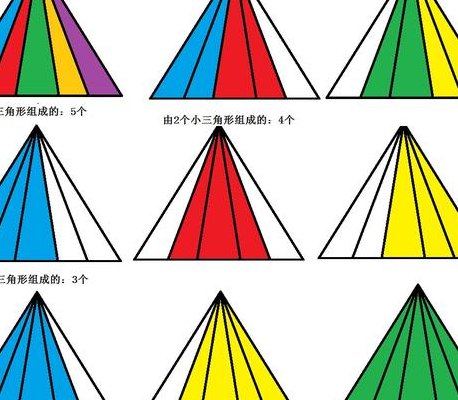
1、总共12个三角形 单独一个的小三角形3个 单独两个部分组成的有5个 三个部分组成的有1个 四个部分组成的有2个 六个部分组成的有1个。

2、单个的三角形：24个；两个部分组成的三角形：20个；三部分组成的三角形：8个；四部分组成的三角形：8个；六部分组成的三角形：4个；八部分组成的三角形：4个；十二部分组成的三角形：4个；共计72个。

3、共有11个：1个图形的有5个+2个图形组成的有5个+3个图形组成的有1个。不论采用什么方法进行统计三角形个数，一定注意不要多算或者漏掉。一定按照规则和次序进行。

4、同理，三角形ACE、三角形ABC同样被分成了六个三角形 所以这一共是18个三角形 三角形DCE、三角形CEB每个三角形被分三个三角形 所以一共是六个三角形 所以这个图形总共有24个三角形。

5、共有24个三角形。如图，以红色线段为底，黑色线段为两条侧边的三角形，共有3层，每层都有6个：3+2+1=6，6×3=18，一共18个。以绿色线段为底，或则蓝色线段为底，黑色线段为两条侧边的三角形，每种有3个，且与前面的没有重复，3×2=6，一共6个。18+6=24，共计24个三角形。

一共有多少个三角形?

1、一共有36个三角形. 理由：因为每个小正方形有四个小三角形组成，所以共有四四十六个小三角形；又因为每个小正方形的每条对角线把小正方形分为两个小三角形，所以共有十六个小三角形；再因为大正方形的两条对角线把大正方形分为两个小三角形。

2、要根据具体题目来分析，比如 解：单个的三角形有8个，4个三角形组成的大三角形一共有2个 8+2=10（个）一共有10个三角形。

3、水平方向的3条线段和一条斜线段共可构成：7×6÷2×4=84个纵向三角形。一条斜线段和底边方向线段共可构成6个横向三角形。共有：84+6=92个三角形。

4、一共十个。外面的五个角组成五个小三角形，中间的五边形，每个内角又可以组成五个大三角形。

5、一共有多少个三角形介绍如下：四十五个三角形。

6、一共有25个三角形，是通过以下步骤推算得到的。据题意可知，由十六个三角形组成一个大三角形，计16个，据图可划出3个三角形，计得19个，据图可划出4个三角形，计得23个，据图可划出2个三角形，总计得到25个三角形。

有多少个三角形

总共12个三角形 单独一个的小三角形3个 单独两个部分组成的有5个 三个部分组成的有1个 四个部分组成的有2个 六个部分组成的有1个。

共有11个：1个图形的有5个+2个图形组成的有5个+3个图形组成的有1个。不论采用什么方法进行统计三角形个数，一定注意不要多算或者漏掉。一定按照规则和次序进行。

一共十个。外面的五个角组成五个小三角形，中间的五边形，每个内角又可以组成五个大三角形。

图形被分别了11块，其中3……10都是三角形。这样，单个的小三角形共有10个。1和2和3和4……9和10和1，两个小三角形组成的较大三角形也有10个。

要根据具体题目来分析，比如 解：单个的三角形有8个，4个三角形组成的大三角形一共有2个 8+2=10（个）一共有10个三角形。

共有24个三角形。如图，以红色线段为底，黑色线段为两条侧边的三角形，共有3层，每层都有6个：3+2+1=6，6×3=18，一共18个。以绿色线段为底，或则蓝色线段为底，黑色线段为两条侧边的三角形，每种有3个，且与前面的没有重复，3×2=6，一共6个。18+6=24，共计24个三角形。

有几个三角形?

1、总共12个三角形 单独一个的小三角形3个 单独两个部分组成的有5个 三个部分组成的有1个 四个部分组成的有2个 六个部分组成的有1个。

2、共有11个：1个图形的有5个+2个图形组成的有5个+3个图形组成的有1个。不论采用什么方法进行统计三角形个数，一定注意不要多算或者漏掉。一定按照规则和次序进行。

3、所以一共是六个三角形 所以这个图形总共有24个三角形。问题五：图中一共有几个三角形？ 13 问题六：一共有多少个三角形？ 我们先从最里面的正方形来看，最小的一共有8个然后再由二分之一的对角线组成的有4个，然后由整条对角线组成的有4个，一共是16个。

4、一共22个三角形。单个的三角形10个，相信你很容易数出来。由两个三角形组成的三角形共8个，上、下的菱形中各有4个。由三个三角形组成的三角形共4个，藏在中间的矩形中。由更多三角形组成的三角形不存在。所以总过：10+8+4=22个三角形。

有多少个三角形?多谢

由五部分(一个五边形和4个三角形)组成的大三角形(如11和6)共5个。这样，图中一共有35个三角形。

解：假设其余两边为x和y 则应当满足x+y11且0x11 和0y11 接着分类讨论即可（实际上很有规律）如x=2，则y=10 1种 x=3，则y=10，9 2种 ……x=6，则y=10，9……，6 5种 显然当x=7时出现重复的情况。

你说的只出现一个三角形，是正常情况下的作图方法，无可厚非，我完全赞同。但是，如果投影方向不是通常情况下的那么正，而是斜了一个角度，那么，就会出现两个或多个三角形。这道题目可以理解为：至少有一个三角形，也可能会出现两个或多个三角形。总觉得，这题好像没啥意思，有点欺骗性。

过每一个顶点跟与它不相邻的任意两个顶点（不包括与它相对的点）构成一个等边三角形，可够成3个。8个顶点共构成8×3=24个。这样，每一个顶点都用了3次，所以可以组成24÷3=8个等边三角形。

画15个☆时应该画14个△；画5个△时画了15个☆。

老师问一下有多少个三角形

1、由3个倒三角形组成的倒三角形有((n-3)^2+n-3)/2个 由6个倒三角形组成的倒三角形有((n-5)^2+n-5)/2个 。。由(m^2+m)/2个倒三角形组成的倒三角形有((n-2m+1)^2+n-2m+1)/2个 。。

2、先数单个的，在数由两个组成的大三角形，以此类推。

3、引言 记得在小学一年级时，老师曾经问过我们一个问题：正方形是由几个三角形组成的？当时大家都很懵，因为这个问题似乎不是我们一年级所学习的内容。然而，正方形作为一种基础的几何形状，它的构成还是有一定的规律可循的。

4、可以包括，正方形和长方形是平行四边形特例，是平行四边形。正方形的个数算长方形的个数；长方形的个数不能算正方形的个数。请采纳，O(∩_∩)O谢谢。

5、引言 记得在小学一年级时，老师曾经问过我们一个问题：正方形是由几个三角形组成的？当时大家都很懵，因为这个问题似乎不是我们一年级所学习的内容。然而，正方形作为一种基础的几何形状，它的构成还是有一定的规律可循的。