圆锥体积公式推导过程（圆锥体积公式推导过程视频实例讲解）

圆锥体积公式推导过程是什么?

圆锥的体积公式推导过程为：圆锥的体积=圆柱体积÷3，而圆柱的体积=底面积×高，所以圆锥的体积V=底面积×高÷3。若圆锥型的容器注满水，倒入圆柱型的容器内，需要三次才能将圆柱型的容器倒满，说明圆锥的体积是圆柱体积的1/3，所以圆锥的体积V=底面积×高÷3。

一个圆锥的体积等于与它等底等高的圆柱的体积的1/3，根据圆柱体积公式V=Sh(V=rrπh)，得出圆锥体积公式：圆锥V=1/3Sh。S是圆锥的底面积，h是圆锥的高，r是圆锥的底面半径。证明：把圆锥沿高分成k分，每份高h/k。第n份半径：n*r/k。第n份底面积：pi*n^2*r^2/k^2。

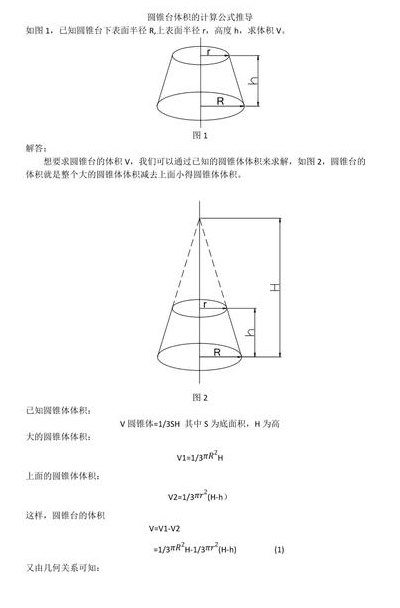
圆锥体的体积由圆柱推导而来。设 h为圆台的高， r和R为棱台的上下底面半径， V 为圆台的体积。由于圆台是由一个平面截去圆锥的一部分（也就是和原来圆锥相似的一个小圆锥）得到，所以计算体积的时候，可以先算出原来圆锥的体积。再减去和它相似的小圆锥的体积。

圆锥体积的推导过程可以追溯到古希腊数学家阿基米德。他通过实验和几何方法证明了圆锥的体积公式，即V=1/3πrh，其中r为底面半径，h为圆锥的高。

圆锥的体积公式推导过程

1、圆锥的体积公式推导过程为：圆锥的体积=圆柱体积÷3，而圆柱的体积=底面积×高，所以圆锥的体积V=底面积×高÷3。若圆锥型的容器注满水，倒入圆柱型的容器内，需要三次才能将圆柱型的容器倒满，说明圆锥的体积是圆柱体积的1/3，所以圆锥的体积V=底面积×高÷3。

2、一个圆锥的体积等于与它等底等高的圆柱的体积的1/3，根据圆柱体积公式V=Sh(V=rrπh)，得出圆锥体积公式：圆锥V=1/3Sh S是圆锥的底面积，h是圆锥的高，r是圆锥的底面半径。

3、圆锥的体积公式是V=1/3πr_h，其中r是底面半径，h是高。这个公式的推导过程可以通过以下步骤进行：首先，我们可以将一个圆锥切成无数个微小的圆柱，每个圆柱的高度等于圆锥的高，底面半径等于圆锥底面的半径。然后，我们考虑这些微小的圆柱的总体积。

4、圆锥体积的推导过程可以追溯到古希腊数学家阿基米德。他通过实验和几何方法证明了圆锥的体积公式，即V=1/3πrh，其中r为底面半径，h为圆锥的高。

5、圆锥体的体积由圆柱推导而来。设 h为圆台的高， r和R为棱台的上下底面半径， V 为圆台的体积。由于圆台是由一个平面截去圆锥的一部分（也就是和原来圆锥相似的一个小圆锥）得到，所以计算体积的时候，可以先算出原来圆锥的体积。再减去和它相似的小圆锥的体积。

圆锥体积公式怎么推导的?

一个圆锥的体积等于与它等底等高的圆柱的体积的1/3，根据圆柱体积公式V=Sh(V=rrπh)，得出圆锥体积公式：圆锥V=1/3Sh。S是圆锥的底面积，h是圆锥的高，r是圆锥的底面半径。证明：把圆锥沿高分成k分，每份高h/k。第n份半径：n*r/k。第n份底面积：pi*n^2*r^2/k^2。

圆锥的体积公式推导过程为：圆锥的体积=圆柱体积÷3，而圆柱的体积=底面积×高，所以圆锥的体积V=底面积×高÷3。若圆锥型的容器注满水，倒入圆柱型的容器内，需要三次才能将圆柱型的容器倒满，说明圆锥的体积是圆柱体积的1/3，所以圆锥的体积V=底面积×高÷3。

用极限法可以推导： V＝1/3Sh（V＝1/3SH）S是底面积，h是高，r是底面半径。设圆锥高为h，底部半径为r，把圆锥等分为k份，每份看做一个小圆柱。则第n份圆柱的高为h/k， 半径为n*r/k。