几何平均（几何平均值）

斐波那契理论

1、斐波那契的原理：斐波那契原理，也称为黄金分割原理，是一种广泛应用于自然界和艺术中的数学原理。斐波拉契数列（又译作“斐波那契数列”或“斐波那切数列”）是一个非常美丽、和谐的数列，它的形状可以用排成螺旋状的一系列正方形来说明起始的正方形(图中用灰色表示)的边长为1。

2、经典理论系列课程波浪理论（五）——斐波那契数列与波浪的关系钟文杰斐波南希数列为波浪理论的结构基础意大利数家列昂纳.斐波那契，在13世纪研究发现了一组神奇数字：1，12358144……直至无限。看似简单的数列，但背后却隐藏着无穷的奥妙，它具有许多的特性。

3、斐波那契数列的定义者，是意大利数学家莱昂纳多·斐波那契（Leonardo Fibonacci），生于公元1170年，卒于1250年，籍贯是比萨。他被人称作“比萨的莱昂纳多”。1202年，他撰写了《算盘全书》（Liber Abacci）一书。他是第一个研究了印度和阿拉伯数学理论的欧洲人。

4、他还曾在埃及、叙利亚、希腊、西西里和普罗旺斯研究数学。斐波那契数列的理论是初等数学中困难而有趣的问题，它与“高深数学”的历史、问题和方法有紧密的联系。从有名的兔子问题开始几乎经历了八百年久远的岁月。迄今为止，斐波那契数列仍然是初等数学中最吸引人的一章。

5、假设一对新生的兔子，从第二个月起开始繁殖，每第个月能生一对兔子，且兔子不死，求n个月后有多少对兔子。通过递推方式可得到第n个月的兔子总数为斐波那契数列的第n+1项。裴波那契数列常数趋于黄金分割比，数学家也进一步拓展了裴波那契数列的理论结构。

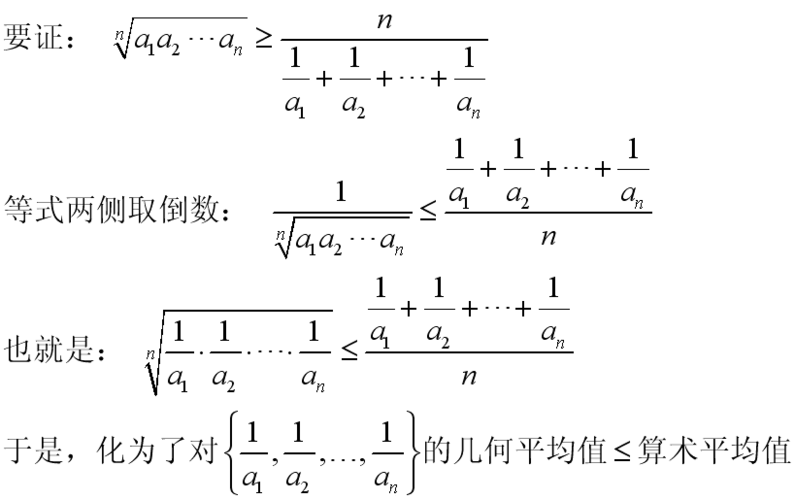
几何平均数是什么?

1、几何平均数是一种用于计算数值集合中所有数值乘积的n次方根的方法。与算术平均数不同，几何平均数考虑的是数值的相对变化而非绝对变化，因此更能反映数值集合的真实情况。具体来说，对于一组数值xx...、xn，其几何平均数G可以通过以下公式计算：G = (x1 * x2 * ... * xn)^(1/n)。

2、几何平均数是n个变量值连乘积的n次方根。求几何平均数的方法叫做几何平均法。如果总水平、总成果等于所有阶段、所有环节水平、成果的连乘积总和时，求各阶段、各环节的一般水平、一般成果，要使用几何平均法计算几何平均数。而不能使用算术平均法计算算术平均数。

3、几何平均数是一种用于计算一组数值的中心趋势的统计量。与算术平均数不同，几何平均数更注重数值的比例关系，因此在处理具有不同单位或百分比的数值时，它通常更为合适。例如，当我们要计算多个投资项目的平均收益率时，由于收益率通常是百分比形式，使用几何平均数可以更准确地反映整体收益情况。

4、几何平均数是对各变量值的连乘积开项数次方根。是n个变量值连乘积的n次方根。

5、几何平均数是N个数据的连乘积的开N次方根。算术平均数是一组数据的代数和除以数据的项数所得的平均数。调和平均数是一组数据的倒数和除数据的项数的倒数。平方平均数是一组数据的平方和除以数据的项数的开方。对同一数据。调和=几何=算术=平方。

6、几何平均数是一种用于计算一组数值的平均值的方法，它的获取方式是取所有数值相乘后的结果，然后取其积的算术平均数。这种方法常用于计算比例数据或者一系列正值的平均数。几何平均数的具体计算方式反映了各数值之间的乘性关系，强调整体的平均乘性强度。

几何平均数的计算公式是什么?

1、总之，几何平均数的计算公式为$G = \sqrt[n]{a_1 \times a_2 \times ... \times a_n}$，它适用于计算一组数值的平均值，特别是在处理比率或百分比数据时更加适用。几何平均数具有稳定性高、应用广泛等特点，在数学、经济学、金融学等领域中得到了广泛应用。

2、几何平均数的计算公式是G=n√X1·X2·...·Xn。几何平均数是n个变量值连乘积的n次方根。几何平均数：几何平均数是对各变量值的连乘积开项数次方根。根据所拿掌握资料的形式不同，其分为简单几何平均数和加权几何平均数两种形式。几何平均数的计算公式是Gn=n√x1x2x3……xn。

3、几何平均数的计算公式是G=(a1a..an)^1/n 几何平均数的计算公式是什么 几何平均数是指n个数值的乘积的n次方根。通常用于计算一组数据的平均值，特别是在需要考虑到数据之间的相关性时。其计算公式为：G=n√[a1a2…an]，其中G表示几何平均数，n表示数据个数，aa…、an表示数据。

4、几何平均值=(x1×x2×x3…×xn)^1/n 其中，x1，x2，x3…xn是样本数据。定义。平均数是统计学中最常用的统计量，用来表明资料中各观测值相对集中较多的中心位置。在畜牧业、水产业生产实践和科学研究中，平均数被广泛用来描述或比较各种技术措施的效果、畜禽某些数量性状的指标等等。

5、几何平均值的计算公式为：n个数据的连乘积再开n次方根。几何平均数是对各变量值的连乘积开项数次方根，求几何平均数的方法叫做几何平均法。几何平均数是n个变量值连乘积的n次方根。