平方根的定义(平方根的定义和性质)
什么叫做平方根
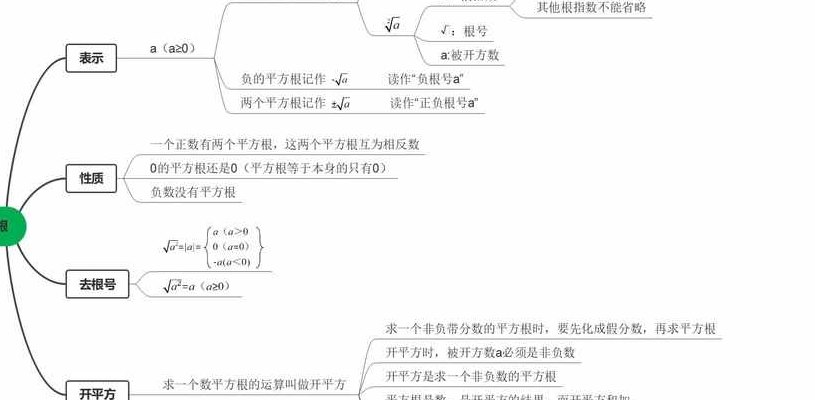
1、平方根,又叫二次方根,表示为〔±√ ̄〕,其中属于非负数的平方根称之为算术平方根(arithmetic square root)。一个正数有两个实平方根,它们互为相反数,负数有两个共轭的纯虚平方根。
2、平方根,又叫二次方根,表示为〔±√ ̄〕,其中属于非负数的平方根称之为算术平方根(arithmetic square root)。一个正数有两个实平方根,它们互为相反数;0只有一个平方根,就是0本身;负数有两个共轭的纯虚平方根。一般地,“√ ̄”仅用来表示算术平方根,即非负数的非负平方根。
3、平方根概念 平方根,又叫二次方根,表示为〔±√ ̄〕,其中属于非负数的平方根称之为算术平方根。一个正数有两个实平方根,它们互为相反数,负数没有平方根,0的平方根是0。负数在实数系内不能开平方。只有在复数系内,负数才可以开平方。负数的平方根为一对共轭纯虚数。
4、平方根的定义:如果一个数的平方等于a,那么这个数叫做平方根或二次方根。算术平方根定义:如果一个非负数x的平方等于a,那么这个非负数x叫做a的算术平方根。其中,a是被开方数。被开方数越大,对应的算术平方根也越大(对所有正数都成立)。
平方根是什么意思?
1、平方根又叫二次方根,数学上指一数自乘,刚好等于某数,则此数即为某数的平方根,也就是将某数开平方所得的数。一个正数如果有平方根,那么必定有两个,它们互为相反数。显然,如果知道了这两个平方根的一个,那么就可以及时的根据相反数的概念得到它的另一个平方根。负数在实数系内不能开平方。
2、平方根是一个数学概念,表示一个数的二次方根。具体来说,一个数的平方根是另一个数,当这个数乘以它自己时,结果等于原来的数。例如,因为4乘以自身等于16,所以4是16的平方根。同样地,因为9乘以自身等于81,所以9是81的平方根。平方根可以是正数或负数,取决于上下文和需要。
3、平方根的意思是指一个数的二次方根,也就是这个数乘以它自己等于原来的数。平方根是一个数学概念,用于表示一个数的二次方程的解。具体来说,一个数的平方根是一个数,当这个数乘以自己时,结果等于原来的数。例如,4的平方根是2,因为2乘以2等于4。同样地,9的平方根是3,因为3乘以3等于9。
4、平方根的解释[square root] 平方时能得出初始量的两个量中的任一个 +3或-3是9的平方根 详细解释 某数的二次方根,如4的平方根是±2。 词语分解 平的解释 平 í 不倾斜,无凹凸,像静止的水面一样:平地。平面。平原。 均等:平分。 平行 (妌 )。抱打不平。 公平 合理。
5、平方根是一个数学概念,又叫二次方根。一个正数有两个实平方根,它们互为相反数,负数在实数范围内没有平方根,0的平方根是0。平方根的定义是,如果一个数x的平方等于a,即x=a,那么这个数x就叫做a的平方根。其中,a叫做被开方数。
6、平方根,又叫二次方根,表示为〔±√ ̄〕,其中属于非负数的平方根称之为算术平方根(arithmetic square root)。一个正数有两个实平方根,它们互为相反数,负数没有平方根,0的平方根是0。开方数越大,对应的算术平方根也越大(对所有正数都成立)。
平方根是如何定义的平方根有哪些特征并举例三个例子?
1、平方根定义:如果一个数的平方等于a,那么这个数叫做a的平方根或二次方根。如果x2=a,那么 x叫做a的平方根,a叫做被开方数。平方根的表示方法:正数a的平方根表示为“a”,读作“正、负根号a”。
2、算术平方根定义:如果一个非负数x的平方等于a,那么这个非负数x叫做a的算术平方根。其中,a是被开方数。被开方数越大,对应的算术平方根也越大(对所有正数都成立)。例如:因为2和-2的平方都是4,且只有2是正数,所以2就是4的算术平方根。0本身是非负数,因此0也是0的算术平方根。
3、非负实数的平方根仍然是非负的实数,但是负实数没有实数的平方根,只有复数的平方根。 平方根是唯一的,每个非负实数都有唯一一个非负实数的平方根。 平方根与平方是相反的运算,即一个数的平方根与这个数的平方互为相反数。例如:(-3)的平方为9,9的平方根为3。
平方根的定义是什么?
平方根的定义:如果一个数的平方等于a,那么这个数叫做平方根或二次方根。算术平方根定义:如果一个非负数x的平方等于a,那么这个非负数x叫做a的算术平方根。其中,a是被开方数。被开方数越大,对应的算术平方根也越大(对所有正数都成立)。
平方根,又叫二次方根,表示为〔±√ ̄〕,其中属于非负数的平方根称之为算术平方根(arithmetic square root)。一个正数有两个实平方根,它们互为相反数,负数有两个共轭的纯虚平方根。
如果一个数x的平方等于a,那么这个数x就叫做a的平方根(或二次方根)。平方根,又叫二次方根,表示为〔±√ ̄〕,其中属于非负数的平方根称之为算术平方根(arithmetic square root)。一个正数有两个实平方根,它们互为相反数,负数有两个共轭的纯虚平方根。
平方根是数学中常用的概念,表示一个数的平方等于给定的数。平方根的定义来源于数学中方程的解的概念。平方根定义:对于非负实数x,若存在一个非负实数y,使得y的平方等于x,则称y为x的平方根。② 知识点运用:平方根在数学和实际生活中有广泛的运用。
平方根,又叫二次方根,对于非负实数来说,是指某个自乘结果等于的实数,表示为〔√ ̄〕,其中属于非负实数的平方根称算术平方根。一个正数有两个平方根;0只有一个平方根,就是0本身;负数没有平方根。 例:9的平方根是±3 注:有时我们说的平方根指算术平方根。
平方根的定义 平方根,又称二次平方根,表示为[ ̄]。非负数的平方根称为算术平方根。正数有两个实数平方根,它们彼此相反,而负数没有平方根。 如果一个数字x的平方等于a,那么这个数字x被称为a的平方根(或二次根)。
平方根的定义
1、平方根,又叫二次方根,表示为〔±√ ̄〕,其中属于非负数的平方根称之为算术平方根(arithmetic square root)。一个正数有两个实平方根,它们互为相反数,负数有两个共轭的纯虚平方根。
2、平方根的定义:如果一个数的平方等于a,那么这个数叫做平方根或二次方根。算术平方根定义:如果一个非负数x的平方等于a,那么这个非负数x叫做a的算术平方根。其中,a是被开方数。被开方数越大,对应的算术平方根也越大(对所有正数都成立)。
3、如果一个数x的平方等于a,那么这个数x就叫做a的平方根(或二次方根)。平方根,又叫二次方根,表示为〔±√ ̄〕,其中属于非负数的平方根称之为算术平方根(arithmetic square root)。一个正数有两个实平方根,它们互为相反数,负数有两个共轭的纯虚平方根。
4、平方根,又叫二次方根,对于非负实数来说,是指某个自乘结果等于的实数,表示为〔√ ̄〕,其中属于非负实数的平方根称算术平方根。一个正数有两个平方根;0只有一个平方根,就是0本身;负数没有平方根。 例:9的平方根是±3 注:有时我们说的平方根指算术平方根。
什么叫平方根的定义
平方根的定义:如果一个数的平方等于a,那么这个数叫做平方根或二次方根。算术平方根定义:如果一个非负数x的平方等于a,那么这个非负数x叫做a的算术平方根。其中,a是被开方数。被开方数越大,对应的算术平方根也越大(对所有正数都成立)。
平方根,又叫二次方根,表示为〔±√ ̄〕,其中属于非负数的平方根称之为算术平方根(arithmetic square root)。一个正数有两个实平方根,它们互为相反数,负数有两个共轭的纯虚平方根。
如果一个数x的平方等于a,那么这个数x就叫做a的平方根(或二次方根)。平方根,又叫二次方根,表示为〔±√ ̄〕,其中属于非负数的平方根称之为算术平方根(arithmetic square root)。一个正数有两个实平方根,它们互为相反数,负数有两个共轭的纯虚平方根。
平方根,又叫二次方根,对于非负实数来说,是指某个自乘结果等于的实数,表示为〔√ ̄〕,其中属于非负实数的平方根称算术平方根。一个正数有两个平方根;0只有一个平方根,就是0本身;负数没有平方根。 例:9的平方根是±3 注:有时我们说的平方根指算术平方根。
平方根是数学中常用的概念,表示一个数的平方等于给定的数。平方根的定义来源于数学中方程的解的概念。平方根定义:对于非负实数x,若存在一个非负实数y,使得y的平方等于x,则称y为x的平方根。② 知识点运用:平方根在数学和实际生活中有广泛的运用。
平方根的定义 平方根,又称二次平方根,表示为[ ̄]。非负数的平方根称为算术平方根。正数有两个实数平方根,它们彼此相反,而负数没有平方根。 如果一个数字x的平方等于a,那么这个数字x被称为a的平方根(或二次根)。