什么是有理数和无理数（什么是有理数和无理数的例子）

什么叫有理数,什么叫无理数

1、无理数：不是有理数的实数称为无理数，即无理数的小数部分是无限不循环的数。

2、有理数的小数部分是有限或为无限循环的数。不是有理数的实数称为无理数，即无理数的小数部分是无限不循环的数。有理数集可以用大写黑正体符号Q代表。但Q并不表示有理数，有理数集与有理数是两个不同的概念。有理数集是元素为全体有理数的集合，而有理数则为有理数集中的所有元素。

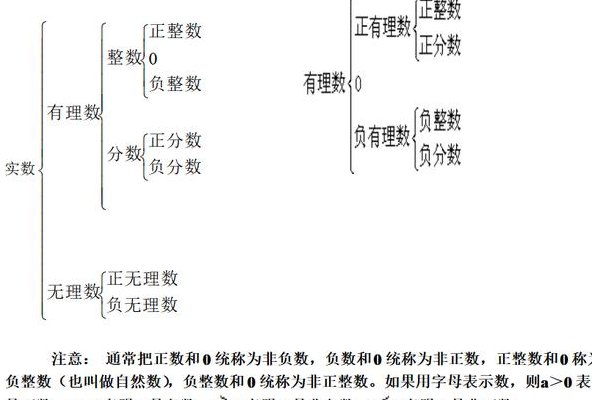
3、有理数是整数（正整数、0、负整数）和分数的统称，是整数和分数的集合。整数也可看做是分母为一的分数。不是有理数的实数称为无理数，即无理数的小数部分是无限不循环的数。

4、有理数的特征：有理数的小数部分是有限或为无限循环的数。无理数的特征：无理数的小数部分是无限不循环的数。两者的实质不同：有理数的实质：有理数为整数（正整数、0、负整数）和分数的统称。正整数和正分数合称为正有理数，负整数和负分数合称为负有理数。

有理数和无理数的区别是什么?

1、有理数和无理数的区别为：小数形式不同，整数之比不同，位数不同等。小数形式不同 把有理数和无理数都写成小数形式时，有理数能写成有限小数和无限循环小数。

2、无理数和有理数的区别有：含义不同、特征不同、实质不同。含义不同 有理数的含义：数学中，有理数是一个整数a和一个正整数b的比，例如3/8，通常为a/b，也是有理数；无理数的含义：在数学中，无理数是所有不是有理数字的 实数，后者是由整数的比率（或分数）构成的数字。

3、有理数和无理数分别指的是：有理数：有理数是整数（正整数、0、负整数）和分数的统称，是整数和分数的集合。整数也可看做是分母为一的分数。不是有理数的实数称为无理数，即无理数的小数部分是无限不循环的数。

4、(1)性质的区别：有理数是两个整数的比，总能写成整数、有限小数或无限循环小数。无理数不能写成两个整数之比，是无限不循环小数。(2)结构的区别：有理数是整数和分数的统称。无理数是所有不是有理数的实数。

5、有理数和无理数的区别(1)性质的区别：有理数是两个整数的比，总能写成整数、有限小数或无限循环小数。无理数不能写成两个整数之比，是无限不循环小数。(2)结构的区别：有理数是整数和分数的统称。无或慎掘理数是所有不是有理数的实数。

有理数、无理数、实数以及什么是复数?

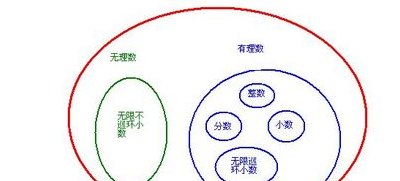
实数，是有理数和无理数的总称。数学上，实数定义为与数轴上的实数，点相对应的数。实数可以直观地看作有限小数与无限小数，实数和数轴上的点一一对应。但仅仅以列举的方式不能描述实数的整体。实数和虚数共同构成复数。虚数 在数学里，将偶指数幂是负数的数定义为纯虚数。所有的虚数都是复数。

实数是有理数和无理数的总称，表示为 a。虚数是复数中除了实数的数。复数就是实数和虚数的总称，所有的数都是复数。实数包括有理数和无理数。有理数主要包括整数、分数、有限小数、无限循环小数，无理数主要包括开方开不尽的数、无限不循环小数。

实数（realnumber）是有理数和无理数的总称。实数定义为与数轴上的实数，点相对应的数。虚数。虚数是指实数以外的复数，其中实部为0的虚数称为纯虚数。在数学中，虚数就是形如a+b*i的数，其中a，b是实数，且b≠0，i=-1。数学上，实数定义为与数轴上的实数，点相对应的数。

实数就是除了虚数以外的所有数的集合，坐标表示就是坐标轴上所有点的集合，虚数就是含有虚部，也就是i的部分的数，其中i是-1的平方根。虚数坐标表示就是在虚平面内除了实轴外所有点的集合 实数分为有理数和无理数，区别在于有理数可以用两个整数之比的形式表示出来，无理数则不能。

什么是无理数和有理数?

1、有理数：有理数分为正有理数，负有理数，0。有理数都可以化为小数，其中整数可以看作小数点后面是零的小数，只要是无限循环小数的都叫有理数。如：12121212121212…… 无理数：无限不循环小数。

2、有理数是整数（正整数、0、负整数）和分数的统称，是整数和分数的集合。整数也可看做是分母为一的分数。不是有理数的实数称为无理数，即无理数的小数部分是无限不循环的数。

3、无限不循环小数和开根开不尽的数叫无理数，整数和分数统称为有理数。包括整数和通常所说的分数，此分数亦可表示为有限小数或无限循环小数。这一定义在数的十进制和其他进位制（如二进制）下都适用。数学上，有理数是一个整数a和一个非零整数b的比(ratio)，通常写作a/b，故又称作分数。

什么是有理数和无理数_百度问一问

您好！亲，有理数呢是指总数和分数的统称有理数是整数和分数的集合。无理数也被称为无限不循环小数，不能写作两整数之比。【摘要】什么是有理数和无理数【提问】您好！亲，有理数呢是指总数和分数的统称有理数是整数和分数的集合。无理数也被称为无限不循环小数，不能写作两整数之比。

有理数和无理数分别指的是：有理数：有理数是整数（正整数、0、负整数）和分数的统称，是整数和分数的集合。整数也可看做是分母为一的分数。不是有理数的实数称为无理数，即无理数的小数部分是无限不循环的数。

有理数的含义：数学中，有理数是一个整数a和一个正整数b的比，例如3/8，通常为a/b，0也是有理数。无理数的含义：在数学中，无理数是所有不是有理数字的实数，后者是由整数的比率（或分数）构成的数字。

有理数是“数与代数”领域中的重要内容之一，在现实生活中有广泛的应用，是继续学习实数、代数式、方程、不等式、直角坐标系、函数、统计等数学内容以及相关学科知识的基础。数学上，有理数是一个整数a和一个正整数b的比，例如3/8，通则为a/b。0也是有理数。

有理数和无理数定义的区别是什么

1、有理数和无理数定义有3点不同：两者的含义不同：有理数的含义：数学中，有理数是一个整数a和一个正整数b的比，例如3/8，通常为a/b，0也是有理数。无理数的含义：在数学中，无理数是所有不是有理数字的实数，后者是由整数的比率（或分数）构成的数字。

2、有理数和无理数分别指的是：有理数：有理数是整数（正整数、0、负整数）和分数的统称，是整数和分数的集合。整数也可看做是分母为一的分数。不是有理数的实数称为无理数，即无理数的小数部分是无限不循环的数。

3、有理数和无理数的区别为：小数形式不同，整数之比不同，位数不同等。小数形式不同 把有理数和无理数都写成小数形式时，有理数能写成有限小数和无限循环小数。