什么是整式（什么是整式方程什么是分式方程）

整式是什么?举例

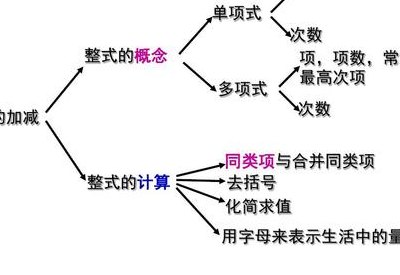
1、单项式和多项式统称为整式。代数式中的一种有理式.不含除法运算或分数，以及虽有除法运算及分数，但除式或分母中不含变数者，则称为整式。整式可以分为定义和运算，定义又可以分为单项式和多项式，运算又可以分为加减和乘除。

2、整式是单项式与多项式的统称，是指可以包含加减乘除运算的数学表达式，在整式中，除了含有加减乘除运算外，还可以包含乘方、括号等运算。整式的分类 单项式是指只含有乘除运算的数学表达式，例如：2x、3y等都是单项式。

3、整式是指由常数、变量和基本运算符组成的代数表达式。常数是不带字母的数，如5等；变量是可以表示任意值的字母，如x、y等；基本运算符包括加法、减法、乘法等。整式的分类 根据变量的次数，整式可以分为零次整式、一次整式、二次整式以及高次整式。零次整式：只包含常数项，没有变量。

“整式”的定义是什么?

单项式与多项式统称为整式。整式的分类 分母中含有字母的式子一定不是多项式也不是单项式，因此其不是整式。所有单项式和多项式都是整式。资料拓展：单项式的定义 由数与字母或字母与字母相乘组成的代数式叫做单项式（monomial）。单独一个数或一个字母也叫单项式，如Q，0，-1，a。也叫常数项。

整式，是指单项式和多项式的统称，是有理式的一部分。在有理式中，可以包含加、减、乘、除、乘方五种运算。但在整式中，除数不能含有字母。其中，整式的加减就是单项式和多项式的加减，可利用去括号法则和合并同类项来完成。例如，3x^2y+1/2x^2y=7/2x^2y。什么是整式 整式，主要包括单项式和多项式。

整式是指由常数、变量和基本运算符（加法、减法、乘法）组成的代数表达式。它是代数学中的重要概念，用于描述数学问题和进行运算。整式的定义与基本要素 整式是指由常数、变量和基本运算符组成的代数表达式。

单项式和多项式统称为整式。代数式中的一种有理式.不含除法运算或分数，以及虽有除法运算及分数，但除式或分母中不含变数者，则称为整式。整式可以分为定义和运算，定义又可以分为单项式和多项式，运算又可以分为加减和乘除。

整式是有理式的一部分，在有理式中可以包含加，减，乘，除四种运算，但在整式中除数不能含有字母。单项式和多项式都统称为整式。总概念 单项式与多项式统称为整式。例题：、、是整式。不是整式 2单项式 概念 由数与字母的积或字母与字母的积所组成的代数式叫做单项式（monomial）。

整式是单项式与多项式的统称，是指可以包含加减乘除运算的数学表达式，在整式中，除了含有加减乘除运算外，还可以包含乘方、括号等运算。整式的分类 单项式是指只含有乘除运算的数学表达式，例如：2x、3y等都是单项式。

什么是整式?

整式是指由常数、变量和基本运算符（加法、减法、乘法）组成的代数表达式。它是代数学中的重要概念，用于描述数学问题和进行运算。整式的定义与基本要素 整式是指由常数、变量和基本运算符组成的代数表达式。

整式，是指单项式和多项式的统称，是有理式的一部分。在有理式中，可以包含加、减、乘、除、乘方五种运算。但在整式中，除数不能含有字母。其中，整式的加减就是单项式和多项式的加减，可利用去括号法则和合并同类项来完成。例如，3x^2y+1/2x^2y=7/2x^2y。什么是整式 整式，主要包括单项式和多项式。

单项式和多项式统称为整式。代数式中的一种有理式.不含除法运算或分数，以及虽有除法运算及分数，但除式或分母中不含变数者，则称为整式。整式可以分为定义和运算，定义又可以分为单项式和多项式，运算又可以分为加减和乘除。

什么是整式

1、整式是指由常数、变量和基本运算符（加法、减法、乘法）组成的代数表达式。它是代数学中的重要概念，用于描述数学问题和进行运算。整式的定义与基本要素 整式是指由常数、变量和基本运算符组成的代数表达式。

2、什么是整式 整式是在数学当中对于单项式和多项式的一种统称方式，在一个式子当中，如果其中包含有除法运算，那么其中除数是一定不能够含有字母的形式的，换句话说，在单项式与多项式当中，其分母是一定不能够含有字母的。

3、整式，是指单项式和多项式的统称，是有理式的一部分。在有理式中，可以包含加、减、乘、除、乘方五种运算。但在整式中，除数不能含有字母。其中，整式的加减就是单项式和多项式的加减，可利用去括号法则和合并同类项来完成。例如，3x^2y+1/2x^2y=7/2x^2y。什么是整式 整式，主要包括单项式和多项式。

4、单项式和多项式统称为整式。代数式中的一种有理式.不含除法运算或分数，以及虽有除法运算及分数，但除式或分母中不含变数者，则称为整式。整式可以分为定义和运算，定义又可以分为单项式和多项式，运算又可以分为加减和乘除。

整式是什么

1、整式是指由常数、变量和基本运算符（加法、减法、乘法）组成的代数表达式。它是代数学中的重要概念，用于描述数学问题和进行运算。整式的定义与基本要素 整式是指由常数、变量和基本运算符组成的代数表达式。

2、整式，是指单项式和多项式的统称，是有理式的一部分。在有理式中，可以包含加、减、乘、除、乘方五种运算。但在整式中，除数不能含有字母。其中，整式的加减就是单项式和多项式的加减，可利用去括号法则和合并同类项来完成。例如，3x^2y+1/2x^2y=7/2x^2y。什么是整式 整式，主要包括单项式和多项式。

3、单项式和多项式统称为整式。代数式中的一种有理式.不含除法运算或分数，以及虽有除法运算及分数，但除式或分母中不含变数者，则称为整式。整式可以分为定义和运算，定义又可以分为单项式和多项式，运算又可以分为加减和乘除。

4、什么是整式 整式是在数学当中对于单项式和多项式的一种统称方式，在一个式子当中，如果其中包含有除法运算，那么其中除数是一定不能够含有字母的形式的，换句话说，在单项式与多项式当中，其分母是一定不能够含有字母的。

5、整式为单项式和多项式的统称，是有理式的一部分，在有理式中可以包含加，减，乘，除、乘方五种运算，但在整式中除数不能含有字母。资料拓展：单项式的定义 由数与字母或字母与字母相乘组成的代数式叫做单项式（monomial）。单独一个数或一个字母也叫单项式，如Q，0，-1，a。也叫常数项。

什么是整式,整式乘法有哪些?

整式是有理式的一部分，在有理式中可以包含加，减，乘，除四种运算，但在整式中除数不能含有字母。单项式和多项式都统称为整式。总概念 单项式与多项式统称为整式。例题：、、是整式。不是整式 2单项式 概念 由数与字母的积或字母与字母的积所组成的代数式叫做单项式（monomial）。

整式是数学中的一个概念，它指的是在表达式中只包含加、减、乘、除和乘方运算的代数式。整式包含加、减、乘、除和乘方运算。这意味着在整式中可以进行基本的数学运算，如加法、减法、乘法、除法和乘方。整式中只包含数字和字母的有限次运算。

单项式和多项式都统称为整式。整式是有理式的一部分，在有理式中可以包含加，减，乘，除、乘方五种运算，但在整式中除数不能含有字母。把一个多项式化为几个最简整式的乘积的形式，这种变形叫做把这个多项式因式分解（也叫作分解因式）。分解因式与整式乘法互逆。总概念：单项式 与多项式统称为整式。

整式乘法是指两个或多个整式之间的相乘运算。详细解释如下：整式是数学代数中的一个基本概念，它包含单项式和多项式。整式乘法实际上就是多项式与多项式相乘的过程。具体来说，整式乘法涉及的是如何将两个或多个整式的乘法进行计算和展开。这一过程涉及应用分配律和乘法结合律，遵循一定的规则进行运算。

整式的乘法是数学中一种基本的运算，涉及将两个或多个整式相乘。具体来说，整式是由常数、变量以及加减乘方运算得到的代数式。整式的乘法遵循特定的法则和运算规律，包括单项式乘单项式、单项式乘多项式以及多项式乘多项式等情况。整式的乘法实质上是乘法分配律在多项式领域的应用。