点到圆上的距离公式（点到圆的距离公式怎么理解）

知道圆的方程怎么求圆外的一点到圆上的距离

1、点到圆周的最大距离=点到圆心的距离+半径 。

2、d为点到圆心的距离，r为半径。公式就是点到点的距离公式，然后与半径r比较大小。

3、解：圆外一点到圆上最远距离就是连接点与圆心之间距离再加上半径 如上图点M就是所求的点 圆的方程可化为(x+4)+(y-1)=5 ∴半径R=√5 圆心O(-4，1)∴最远距离PM=OP+R =5+√有问题请追问。。

4、连接园外的点和圆心（该线段交圆的点，最短），延长至圆的另一边（该交点最长）。P 是圆外任意一点，O为圆心，连接PO，与圆交于A ，B 两点，A1是圆上异与A ，B两点的任意一点。

5、点到圆的距离公式为：设点（x，y），那么点到圆的距离d=根号下（x+y）。点到圆心的距离公式也就是两点间距离公式，因为点到圆的距离实际计算的是点到圆心的距离。

圆心到圆上一点的距离公式

1、一 标准方程 (x-a)^2+(y-b)^2=r^2 在平面直角坐标系中，设有圆O，圆心O(a，b) 点P(x，y)是圆上任意一点。因为圆是所有到圆心的距离等于半径的点的集合。

2、点到圆的距离公式为：设点（x，y），那么点到圆的距离d=根号下（x_+y_）。

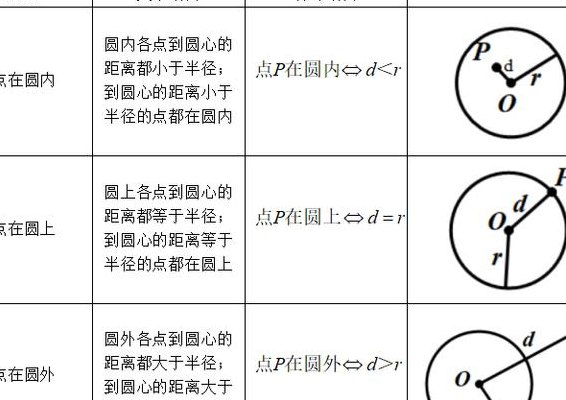
3、如果(x0-a)+(y0-b)r，则P在圆内。如果(x0-a)+(y0-b)=r，则P在圆上。如果(x0-a)+(y0-b)r，则P在圆外。

怎么求圆心和圆上任意一点的距离公式呢?

P在圆O外，则 POr。P在圆O上，则 PO=r。P在圆O内，则 POr。反之亦然。平面内，点P(x0，y0)与圆(x-a)+(y-b)=r的位置关系判断一般方法是：如果(x0-a)+(y0-b)r，则P在圆内。

(x-a)^2+(y-b)^2=r^2 在平面直角坐标系中，设有圆O，圆心O(a，b) 点P(x，y)是圆上任意一点。因为圆是所有到圆心的距离等于半径的点的集合。

计算公式是：D = 2r。其中“D”代表直径，“r”代表半径。公式可变换为r = D/2。方法 2： 已知周长求半径；周长公式是C= 2πr，其中“r”代表半径，π是圆周率（14.）。换算成半径公式就是r = C/2π。方法 3： 已知面积计算半径；圆的面积A = πr2（这里是平方）。

“从圆心到圆上任意一点的距离都相等”是正确的。从圆心到圆上任意一点的距离是指圆的半径，圆的半径有无数条，圆形可以看做是无数个到圆心距离相等的点组成的图形。这是圆形这种图案的基本性质。

点到圆心的距离公式是什么?

点到圆的距离公式为：设点（x，y），那么点到圆的距离d=根号下（x+y）。点到圆心的距离公式也就是两点间距离公式，因为点到圆的距离实际计算的是点到圆心的距离。

点到圆心的距离公式可以通过使用勾股定理来推导得到。假设有一个圆，圆心坐标为 (x， y)，点的坐标为 (x， y)。

P在圆O外，则 POr。P在圆O上，则 PO=r。P在圆O内，则 POr。反之亦然。平面内，点P(x0，y0)与圆(x-a)+(y-b)=r的位置关系判断一般方法是：如果(x0-a)+(y0-b)r，则P在圆内。