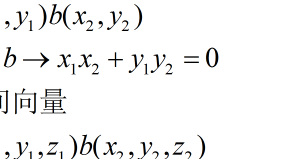两向量垂直（两向量垂直的充要条件是数量积为零）

向量垂直性质有哪些?

两个向量相互垂直性质如下：a·b=0，即向量a与向量b的数量积为0 ；若向量a为（x1，y1），向量b为（x2，y2），则有：(x1x2+y1y2)=0 。

两个向量相互垂直（即正交）时，有以下性质： 数量积为零：如果向量 A（x1，y1）与向量 B（x2，y2）相互垂直，那么它们的数量积为零，即 A·B=0。

两个向量垂直，有垂直定理：若设a=(x1，y1)，b=(x2，y2) ，a⊥b的充要条件是a·b=0，即(x1x2+y1y2)=0 。向量其他定理 向量共线定理 若b≠0，则a//b的充要条件是存在唯一实数λ，使，若设a=(x1，y1)，b=(x2，y2) ，则有 ，与平行概念相同。平行于任何向量。

向量垂直公式

向量垂直公式：a，b是两个向量，a=（a1，a2），b=（b1，b2）a//b：a1/b1=a2/b2或a1b1=a2b2或a=λb，λ是一个常数。a垂直b：a1b1+a2b2=0。向量最初被应用于物理学，很多物理量如力、速度、位移以及电场强度、磁感应强度等都是向量。

向量垂直公式 向量a=（a1，a2），向量b=（b1，b2）。a//b：a1/b1=a2/b2或a1b1=a2b2或a=λb（λ是一个常数）。a垂直b：a1b1+a2b2=0。向量平行公式 向量a=(x1，y1)，向量b=(x2，y2)。x1y2-x2y1=0。a⊥b的充要条件是a·b=0，即(x1x2+y1y2)=0。

向量的垂直公式是：如果两个向量a和b垂直，则它们的点积为0，即ab = 0。向量的平行公式是：如果两个向量a和b平行（或共线），则存在一个实数k，使得b = ka。向量垂直的公式是基于向量的点积运算得出的。点积是两个向量之间的一种运算，其结果是一个标量。

向量a平行向量b的公式和垂直公式分别为：两个向量a，b平行：a=λb （b不是零向量）；两个向量垂直：数量积为0，即　ab=0，坐标表示：a=(x1，y1)，b=(x2，y2)，a//b当且仅当x1y2-x2y1=0，a⊥b当且仅当x1x2+y1y2=0。

两个向量垂直，有垂直定理：若设a=(x1，y1)，b=(x2，y2) ，a⊥b的充要条件是a·b=0，即(x1x2+y1y2)=0 。向量其他定理 向量共线定理 若b≠0，则a//b的充要条件是存在唯一实数λ，使，若设a=(x1，y1)，b=(x2，y2) ，则有 ，与平行概念相同。平行于任何向量。

两向量的垂直与平行公式。

1、向量垂直公式 向量a=（a1，a2），向量b=（b1，b2）。a//b：a1/b1=a2/b2或a1b1=a2b2或a=λb（λ是一个常数）。a垂直b：a1b1+a2b2=0。向量平行公式 向量a=(x1，y1)，向量b=(x2，y2)。x1y2-x2y1=0。a⊥b的充要条件是a·b=0，即(x1x2+y1y2)=0。

2、a×b=xn-ym=0 向量垂直，平行的公式为：若a，b是两个向量：a＝（x，y）b＝（m，n）；则a⊥b的充要条件是a·b=0，即(xm+yn)=0；向量平行的公式为：a//b→a×b=xn-ym=0；向量介绍 “向量”一词来自力学、解析几何中的有向线段。最先使用有向线段表示向量的是英国大科学家牛顿。

3、向量a平行向量b的公式和垂直公式分别为：两个向量a，b平行：a=λb （b不是零向量）；两个向量垂直：数量积为0，即　ab=0，坐标表示：a=(x1，y1)，b=(x2，y2)，a//b当且仅当x1y2-x2y1=0，a⊥b当且仅当x1x2+y1y2=0。

随机（正弦）振动

正弦振动是一种确定性的振动，其任一时刻的状态是可以计算得到的，而且是一个确定的数值。随机振动的是一种非确定性的振动，预选是不可能确定物体上某一时刻的运动瞬时值，只服从统计规律。由于随机振动包涵频谱内所有的频率，所以样品上的共振点会同时激发并可能相互影响，所以试验比同量级的正弦试验严酷。

随机振动和正弦振动区别 随机振动的频带宽，且有连续的频谱，能同时在所有的频率上对试件进行激励，远比正弦振动仅对某些频率或连续扫频来模拟实际环境振动的影响更严酷、更真实和更有效。因此，利用随机振动来考核产品才能更真实地反映产品对振动环境的适应性和考核其结构的完好性。

在筛选实验中，在同种振动量级和同样时间条件下，是不是随机振动对所有的产品的筛选度都比正弦振动要大。

如果你说的汽车的话，随机激励应该模拟的是车辆在路面上行驶时的普遍的一个振动情况。用随机振动通常是为了研究车辆系统的振动特征，减振性能，特振动传递特性的，如果对车辆进行运行平稳性评价，要用规定的道路谱。至于正弦激励通常用于研究车辆对某些频率振动的减振特性的，并非用于模拟形式过程的实际情况。

振动测试指的是仿真产品的运输以及安装还有使用环境里面所受的各种振动环境的影响，可以确定产品能够承受的振动的环境。振动测试也分为正弦振动，跟随机振动。振动测试需要的条件也有很多标准。振动测试主要测试的是电池或者机械产品以及移动电源等等。

两向量垂直的公式是什么?

1、向量垂直公式：a，b是两个向量，a=（a1，a2），b=（b1，b2）a//b：a1/b1=a2/b2或a1b1=a2b2或a=λb，λ是一个常数。a垂直b：a1b1+a2b2=0。向量最初被应用于物理学，很多物理量如力、速度、位移以及电场强度、磁感应强度等都是向量。

2、向量的垂直公式是：如果两个向量a和b垂直，则它们的点积为0，即ab = 0。向量的平行公式是：如果两个向量a和b平行（或共线），则存在一个实数k，使得b = ka。向量垂直的公式是基于向量的点积运算得出的。点积是两个向量之间的一种运算，其结果是一个标量。

3、两个向量垂直，有垂直定理：若设a=(x1，y1)，b=(x2，y2) ，a⊥b的充要条件是a·b=0，即(x1x2+y1y2)=0 。向量其他定理 向量共线定理 若b≠0，则a//b的充要条件是存在唯一实数λ，使，若设a=(x1，y1)，b=(x2，y2) ，则有 ，与平行概念相同。平行于任何向量。

4、该概念垂直公式是：x1x2+y1y2=0。平行公式是：x1y2-x2y1=0。

5、向量a平行向量b的公式和垂直公式分别为：两个向量a，b平行：a=λb （b不是零向量）；两个向量垂直：数量积为0，即　ab=0，坐标表示：a=(x1，y1)，b=(x2，y2)，a//b当且仅当x1y2-x2y1=0，a⊥b当且仅当x1x2+y1y2=0。