椭圆的焦点怎么求（椭圆的焦点怎么算?）

椭圆焦点坐标怎么求

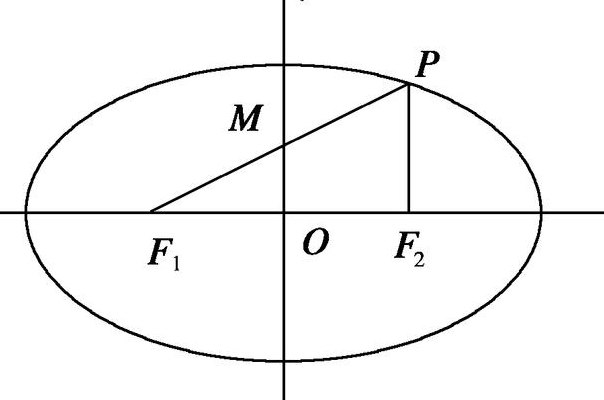
1、椭圆的焦点坐标公式c=√（a^2-b^2）。椭圆的焦点坐标公式：对于椭圆的长轴a和短轴b，焦点到中心的距离c可以通过公式计算：c=√（a^2-b^2），椭圆的焦点坐标为（±c，0）。椭圆是一种圆锥曲线，它可以看作是由围绕其焦点的平面截取圆锥得到的。

2、椭圆焦点坐标：c的平方等于a的平方减b的平方，c是焦点到原点的距离。当焦点在x轴时，椭圆的标准方程是：x^2/a^2+y^2/b^2=1，(ab0)。当焦点在y轴时，椭圆的标准方程是：y^2/a^2+x^2/b^2=1，(ab0)。其中a^2-c^2=b^2 PF1+PF2F1F2(P为椭圆上的点，F为焦点)。

3、椭圆的焦点求法如下：焦点在横轴上时：焦点的纵坐标为0。椭圆长轴的平方减去椭圆短轴的平方，然后开方，将所得结果取正负值，即可得到两个焦点的横坐标。焦点在纵轴上时：焦点的横坐标为0。椭圆长轴的平方减去椭圆短轴的平方，然后开方，将所得结果取正负值，即可得到两个焦点的纵坐标。

4、椭圆焦点坐标公式是a^2-b^2=c^2，其中a为长轴长，b为短轴长，c为焦距。如果长轴长在x轴上的话，焦距为(C，0)，(-C，0），如果长轴长在y轴上的话，焦距为（0，C)，(0，-C)。在数学中，椭圆是平面上到两个固定点的距离之和是常数的轨迹。这两个固定点叫做焦点。

5、椭圆的焦点坐标公式：a^2-b^2=c^2。椭圆（Ellipse）是平面内到定点FF2的距离之和等于常数（大于|F1F2|）的动点P的轨迹，FF2称为椭圆的两个焦点。在几何，焦点（focus或foci）（英国：/foka/，美国：/fosa/）中，焦点是指构建曲线的特殊点。

6、当椭圆的焦点在X轴上：顶点坐标为（a，0）（-a，0）（0，b）（0，-b）当椭圆的焦点在y轴上：顶点坐标为（0，a）（0，-a）（b，0）（-b，0）椭圆上任意一点到F1，F2距离的和为2a，F1，F2之间的距离为2c。而公式中的b=a-c。

椭圆求焦点的计算公式

计算公式为：a^2-b^2=c^2 如果长轴长在x轴上的话，焦距为(C，0)，(-C，0），如果长轴长在y轴上的话，焦距为（0，C)，(0，-C)。其中：长轴长为：2a；短轴长为：2b；焦距为：2c。

椭圆的焦点坐标公式c=√（a^2-b^2）。椭圆的焦点坐标公式：对于椭圆的长轴a和短轴b，焦点到中心的距离c可以通过公式计算：c=√（a^2-b^2），椭圆的焦点坐标为（±c，0）。椭圆是一种圆锥曲线，它可以看作是由围绕其焦点的平面截取圆锥得到的。

椭圆方程：x^2/a^2+y^2/b^2=1；(ab0)所以c^2=a^2-b^2；故焦点是，(c，0)，(-c，0)；椭圆的焦点求法如下：焦点在横轴上时：焦点的纵坐标为0。椭圆长轴的平方减去椭圆短轴的平方，然后开方，将所得结果取正负值，即可得到两个焦点的横坐标。焦点在纵轴上时：焦点的横坐标为0。

根据a^2-b^2=c^2，其中a为长轴长，b为短轴长，c为焦距。如果长轴长在x轴上的话，焦距为(C，0)，(-C，0），如果长轴长在y轴上的话，焦距为（0，C)，(0，-C)。

基本公式法 对于椭圆的标准方程，我们可以通过公式直接求得焦点。已知椭圆的标准方程为frac{x}{a} + frac{y}{b} = 1，其中a为长轴半径，b为短轴半径。焦点距离c的公式为：c = a - b。焦点的位置即可通过此公式求得。

椭圆的标准方程是：y^2/a^2+x^2/b^2=1，(ab0)；其中a^2-c^2=b^2 推导：PF1+PF2F1F2(P为椭圆上的点，F为焦点)平面内到定点FF2的距离之和等于常数（大于|F1F2|）的动点P的轨迹，FF2称为椭圆的两个焦点。其数学表达式为：|PF1|+|PF2|=2a（2a|F1F2|）。

怎么求椭圆的焦点呀

1、椭圆的焦点求法如下：基本公式法 对于椭圆的标准方程，我们可以通过公式直接求得焦点。已知椭圆的标准方程为frac{x}{a} + frac{y}{b} = 1，其中a为长轴半径，b为短轴半径。焦点距离c的公式为：c = a - b。

2、椭圆的焦点求法如下：焦点在横轴上时：焦点的纵坐标为0。椭圆长轴的平方减去椭圆短轴的平方，然后开方，将所得结果取正负值，即可得到两个焦点的横坐标。焦点在纵轴上时：焦点的横坐标为0。椭圆长轴的平方减去椭圆短轴的平方，然后开方，将所得结果取正负值，即可得到两个焦点的纵坐标。

3、如果长轴长在x轴上的话，焦距为(C，0)，(-C，0），如果长轴长在y轴上的话，焦距为（0，C)，(0，-C)。

椭圆的焦点怎么求?

椭圆的焦点求法如下：基本公式法 对于椭圆的标准方程，我们可以通过公式直接求得焦点。已知椭圆的标准方程为frac{x}{a} + frac{y}{b} = 1，其中a为长轴半径，b为短轴半径。焦点距离c的公式为：c = a - b。

椭圆的焦点求法如下：焦点在横轴上时：焦点的纵坐标为0。椭圆长轴的平方减去椭圆短轴的平方，然后开方，将所得结果取正负值，即可得到两个焦点的横坐标。焦点在纵轴上时：焦点的横坐标为0。椭圆长轴的平方减去椭圆短轴的平方，然后开方，将所得结果取正负值，即可得到两个焦点的纵坐标。

焦点在X轴时，标准方程为：x^2/a^2+y^2/b^2=1。焦点在Y轴时，标准方程为：x^2/b^2+y^2/a^2=1。椭圆焦半径公式x=a+ex1，x2=a-ex1。其中a0，b0.a、b中较大者为椭圆长半轴长，较短者为短半轴长。

椭圆的焦点坐标公式c=√（a^2-b^2）。椭圆的焦点坐标公式：对于椭圆的长轴a和短轴b，焦点到中心的距离c可以通过公式计算：c=√（a^2-b^2），椭圆的焦点坐标为（±c，0）。椭圆是一种圆锥曲线，它可以看作是由围绕其焦点的平面截取圆锥得到的。

根据a^2-b^2=c^2，其中a为长轴长，b为短轴长，c为焦距。如果长轴长在x轴上的话，焦距为(C，0)，(-C，0），如果长轴长在y轴上的话，焦距为（0，C)，(0，-C)。

椭圆的焦半径：MF1=a+ex0，MF2=a-ex0，X0为M的横坐标。焦半径公式的推导：利用双曲线的第二定义，设双曲线其左右焦点，则由第二定义：同理即有焦点在x轴上的双曲线的焦半径公式，同理有焦点在y轴上的双曲线的焦半径公式。其中分别是双曲线的下上焦点。

椭圆的圆心和半径怎么求?

1、椭圆的圆心和半径公式如下：焦点在X轴时，标准方程为：x^2/a^2+y^2/b^2=1。焦点在Y轴时，标准方程为：x^2/b^2+y^2/a^2=1。椭圆焦半径公式x=a+ex1，x2=a-ex1。其中a0，b0.a、b中较大者为椭圆长半轴长，较短者为短半轴长。

2、如果给定了一个椭圆的长轴和短轴，它的标准方程是：x/a+y/b=1（a是半长轴，b是半短轴），那么，半焦距 c=a—b所以，这就是求焦点的方法。

3、弧长计算公式是一个数学公式，为L=n（圆心角度数）× π（1）× r（半径）/180（角度制），L=α（弧度）× r(半径) （弧度制）。其中n是圆心角度数，r是半径，L是圆心角弧长。